
【題目】某公司想了解對某產品投入的宣傳費用與該產品的營業額的影響.下面是以往公司對該產品的宣傳費用![]() (單位:萬元)和產品營業額
(單位:萬元)和產品營業額![]() (單位:萬元)的統計折線圖.
(單位:萬元)的統計折線圖.

(Ⅰ)根據折線圖可以判斷,可用線性回歸模型擬合宣傳費用![]() 與產品營業額
與產品營業額![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(Ⅱ)建立產品營業額![]() 關于宣傳費用
關于宣傳費用![]() 的歸方程;
的歸方程;
(Ⅲ)若某段時間內產品利潤![]() 與宣傳費
與宣傳費![]() 和營業額
和營業額![]() 的關系為
的關系為![]() ,應投入宣傳費多少萬元才能使利潤最大,并求最大利潤.
,應投入宣傳費多少萬元才能使利潤最大,并求最大利潤.
參考數據: ![]() ,
, ![]() ,
, ![]() ,
, 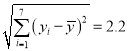 ,
, ![]()
參考公式:相關系數, 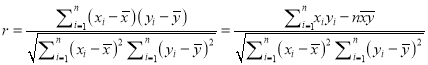 ,
,
回歸方程![]() 中斜率和截距的最小二乘佔計公式分別為
中斜率和截距的最小二乘佔計公式分別為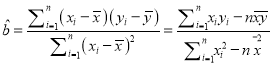 ,
, ![]() .(計算結果保留兩位小數)
.(計算結果保留兩位小數)
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】閱讀如圖所示的程序框圖,解答下列問題:
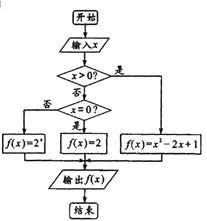
(1)求輸入的![]() 的值分別為
的值分別為![]() 時,輸出的
時,輸出的![]() 的值;
的值;
(2)根據程序框圖,寫出函數![]() (
(![]() )的解析式;并求當關于
)的解析式;并求當關于![]() 的方程
的方程![]() 有三個互不相等的實數解時,實數
有三個互不相等的實數解時,實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·全國Ⅱ卷)如圖,四棱錐P-ABCD中,側面PAD為等邊三角形且垂直于底面ABCD,AB=BC=![]() AD,∠BAD=∠ABC=90°,E是PD的中點.
AD,∠BAD=∠ABC=90°,E是PD的中點.

(1)證明:直線CE∥平面PAB;
(2)點M在棱PC上,且直線BM與底面ABCD所成角為45°,求二面角M-AB-D的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)與函數g(x)的圖像關于原點對稱,且f(x)=![]() +2x, 若函數F(x)=g(x)-
+2x, 若函數F(x)=g(x)-![]() f(x)+1在區間
f(x)+1在區間![]() 上是增函數,求實數
上是增函數,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 與圓C:
與圓C:![]() 相交,截得的弦長為
相交,截得的弦長為![]() .
.
(1)求圓C的方程;
(2)過原點O作圓C的兩條切線,與函數![]() 的圖象相交于M、N兩點(異于原點),證明:直線
的圖象相交于M、N兩點(異于原點),證明:直線![]() 與圓C相切;
與圓C相切;
(3)若函數![]() 圖象上任意三個不同的點P、Q、R,且滿足直線
圖象上任意三個不同的點P、Q、R,且滿足直線![]() 和
和![]() 都與圓C相切,判斷線
都與圓C相切,判斷線![]() 與圓C的位置關系,并加以證明.
與圓C的位置關系,并加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的方程為![]() ,
,![]() 為橢圓C的左右焦點,離心率為
為橢圓C的左右焦點,離心率為![]() ,短軸長為2。
,短軸長為2。
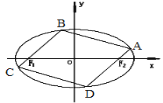
(1)求橢圓C的方程;
(2)如圖,橢圓C的內接平行四邊形ABCD的一組對邊分別過橢圓的焦點![]() ,求該平行四邊形ABCD面積的最大值.
,求該平行四邊形ABCD面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
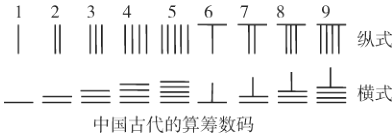
【題目】中國有個名句“運籌帷幄之中,決勝千里之外”,其中的“籌”原意是指《孫子算經》中記載的算籌.古代是用算籌來進行計算,算籌是將幾寸長的小竹棍擺在平面上進行運算,算籌的擺放形式有縱橫兩種形式,(如圖所示),表示一個多位數時,像阿拉伯計數一樣,把各個數位的數碼從左到右排列,但各位數碼的籌式需要縱橫相間,個位、百位、萬位數用縱式表示,十位、千位、十萬位用橫式表示,以此類推.例如8455用算籌表示就是![]() ,則以下用算籌表示的四位數正確的為( )
,則以下用算籌表示的四位數正確的為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一對夫婦為了給他們的獨生孩子支付將來上大學的費用,從孩子一周歲生日開始,每年到銀行儲蓄![]() 元一年定期,若年利率為
元一年定期,若年利率為![]() 保持不變,且每年到期時存款(含利息)自動轉為新的一年定期,當孩子18歲生日時不再存入,將所有存款(含利息)全部取回,則取回的錢的總數為
保持不變,且每年到期時存款(含利息)自動轉為新的一年定期,當孩子18歲生日時不再存入,將所有存款(含利息)全部取回,則取回的錢的總數為![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com