【題目】已知橢圓C：
過點A（﹣1，
），B（
），F為橢圓C的左焦點．
（Ⅰ）求橢圓C的標準方程；
（Ⅱ）若點B為直線l1：x+y+2＝0與直線l2：2x﹣y+4＝0的交點，過點B的直線1與橢圓C交于D，E兩點，求△DEF面積的最大值，以及此時直線l的方程．
【答案】（Ⅰ）
；（Ⅱ）△DEF面積的最大值
，直線l的方程
．
【解析】
（Ⅰ）由橢圓所過定點，待定系數法列方程組能求出橢圓C的標準方程．
（Ⅱ）聯立方程得出B點坐標，根據直線過定點設出過B點的直線，與橢圓聯立，利用韋達定理、弦長公式、不等式性質，結合已知條件能求出△DEF面積的最大值S，并能求出相應的直線方程．
（1）∵橢圓C：
＝1（a＞b＞0）過點A（﹣1，
），B（
），F為橢圓C的左焦點．
∴
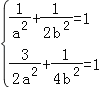，解得a2＝2，b2＝1，
∴橢圓C的標準方程為
＝1．
（Ⅱ）點B為直線l1：x+y+2＝0與直線l2：2x﹣y+4＝0的交點，
聯立
，得B（﹣2，0），
設D（x1，y1），E（x2，y2），由題意設直線l的方程為x＝my﹣2，
代入橢圓方程得（m2+2）y2﹣4my+2＝0，
則△＝16m2﹣8（m2+2）＝8m2﹣16＞0，∴m2＞2，
，y1y2＝
，
∴S△DEF＝S△BEF﹣S△BDF＝
|BF||y1﹣y2|＝
＝
≤
，
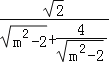當且僅當
＝
，即m2＝6（滿足△＞0）時取得等號，
∴△DEF面積的最大值S＝
，
此時直線1的方程為x＝
，即y＝
（x+2）．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】為調查某地區老年人是否需要志愿者提供幫助，用簡單隨機抽樣的方法從該地區調查了500位老年人，結果如下：
性別 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附：
的觀測值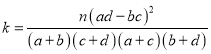
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（1）估計該地區老年人中，需要志愿者提供幫助的老年人的比例；
（2）在犯錯誤的概率不超過0.01的前提下是否可認為該地區的老年人是否需要志愿者提供幫助與性別有關？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝sin（
）的圖象與函數g（x）的圖象關于x＝1對稱，則函數g（x）在（﹣6，﹣4）上（ ）
A. 單調遞增 B. 單調遞減 C. 先增后減 D. 先減后增
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知平面四邊形MNPQ中，MN＝
，MP＝1，MP⊥MN，PQ⊥QM．
（Ⅰ）若PQ＝
，求NQ的值；
（Ⅱ）若∠MQN＝30°，求sin∠QMP的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
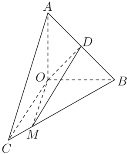
【題目】如圖，在直角△
中，
，△
通過△以直線
為軸順時針旋轉120°得到（
），點
為線段
上一點，且
.
（1）求證：
，并證明：
平面；
（2）分別以
、
、為
、
、
軸建立空間直角坐標系
，求異面直線
與
所成角的大小（用反余弦運算表示）；
（3）若
，求銳二面角
的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
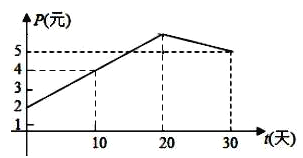
【題目】某上市股票在30天內每股的交易價格P（元）與時間t（天）組成有序數對
，點落在如圖所示的兩條線段上.該股票在30天內（包括30天）的日交易量M（萬股）與時間t（天）的部分數據如下表所示：
第t天 | 6 | 13 | 20 | 27 |
M（萬股） | 34 | 27 | 20 | 13 |
（1）根據提供的圖象，寫出該股票每股交易價格P（元）與時間t（天）所滿足的函數關系式
______；
（2）根據表中數據，寫出日交易量M（萬股）與時間t（天）的一次函數關系式：
______；
（3）用y（萬元）表示該股票日交易額，寫出y關于t的函數關系式，并求在這30天內第幾天日交易額最大，最大值為多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某輪船公司的一艘輪船每小時花費的燃料費與輪船航行速度的平方成正比，比例系數為
輪船的最大速度為15海里
小時
當船速為10海里小時，它的燃料費是每小時96元，其余航行運作費用（不論速度如何)總計是每小時150元假定運行過程中輪船以速度v勻速航行．
求k的值；
求該輪船航行100海里的總費用
燃料費
航行運作費用
的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
