Question

已知△ABC的三邊長分別是3、4、5,點P是它的內切圓上一點,求以PA、PB、PC分別為直徑的三個圓面積之和的最大值和最小值.

Answer 1

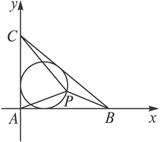
解析:由已知得△ABC為直角三角形,建立如下圖所示的直角坐標系,則A(0,0)、B(4,0)、C(0,3).

設內切圓半徑為r,則r=(a+b-c)=1,故內切圓的方程為(x-1)²+(y-1)²=1.

又設P點坐標為(1+cosα,1+sinα),以PA、PB、PC為直徑的三個圓面積

S=π()²+π()²+π()²

=(PA²+PB²+PC²)

=［(1+cosα)²+(1+sinα)²+(1+cosα-4)²+(1+sinα)²+(1+cosα)²+(1+sinα-3)²］

= (10-cosα),

又∵-1≤cosα≤1,∴當cosα=-1時,S_max=;當cosα=1時,S_min=.