
【題目】數列{an}的前n項和為![]() ,且滿足
,且滿足![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求數列{an}的通項公式;
(2)記![]() ,
,![]() .
.
①求Tn;
②求證:![]() .
.
【答案】(1)![]() (2)①
(2)①![]() ②證明見解析;
②證明見解析;
【解析】
(1)利用公式![]() 得到
得到![]() ,再迭代一次得到數列{an}為等差數列,計算得到答案.
,再迭代一次得到數列{an}為等差數列,計算得到答案.
(2)![]() ,利用裂項相消法得到
,利用裂項相消法得到![]() ,轉化為
,轉化為 ,構造函數
,構造函數![]() ,計算函數單調性得到證明.
,計算函數單調性得到證明.
(1)因為![]() ,所以n=2時,S1=1,即a1=1.
,所以n=2時,S1=1,即a1=1.
因為n≥2時,![]() ,即
,即![]() ,
,![]() 時也適合該式.
時也適合該式.
所以n≥2時,![]() ,
,![]() ,
,
兩式相減得![]() ,則
,則![]() ,
,
兩式相減得![]() ,n≥2.
,n≥2.
所以![]() ,n≥2,所以
,n≥2,所以![]() .
.
所以數列{an}為等差數列,因為a1=1,a2=2,所以公差d=1,所以![]() .
.
(2)①因為an=n,所以![]()
![]() ,
,
所以![]()
![]() ,
,
②要證![]() ,只要證
,只要證![]() ,
,
只要證![]() ,即證
,即證 .
.
設![]() ,x>1,令
,x>1,令![]() ,x>1,則
,x>1,則![]() ,
,
設![]() ,
,![]() ,則
,則![]() ,函數單調遞增,
,函數單調遞增,
故![]() ,故x>1時,
,故x>1時,![]() ,故
,故![]() 在
在![]() 恒成立.
恒成立.
所以![]() 在
在![]() 上單調遞增,
上單調遞增,
因為![]() ,所以
,所以![]() ,所以所證不等式成立.
,所以所證不等式成立.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數學 來源: 題型:
【題目】2020年寒假是特殊的寒假,因為疫情全體學生只能在家進行網上在線學習,為研究學生網上學習的情況,某校社團對男女各10名學生進行了網上在線學習的問卷調查,每名學生給出評分(滿分100分),得到如圖所示的莖葉圖.
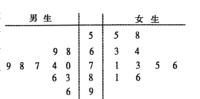
(1)根據莖葉圖判斷男生組和女生組哪個組對網課的評價更高?并說明理由;
(2)如圖是按該20名學生的評分繪制的頻率分布直方圖,求![]() 的值并估計這20名學生評分的平均值(同一組中的數據用該組區間中點值作為代表);
的值并估計這20名學生評分的平均值(同一組中的數據用該組區間中點值作為代表);
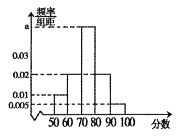
(3)求該20名學生評分的中位數![]() ,并將評分超過
,并將評分超過![]() 和不超過
和不超過![]() 的學生數填入下面的列聯表:
的學生數填入下面的列聯表:
超過 | 不超過 | |
男生 | ||
女生 |
根據列聯表,能否有![]() 的把握認為男生和女生的評分有差異?
的把握認為男生和女生的評分有差異?
附: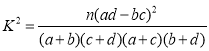 ,
,
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合M是滿足下列性質的函數f(x)的全體:存在非零常數T,對任意x∈R,有f(x+T)=Tf(x)成立.
(1)函數f(x)=x是否屬于集合M?說明理由;
(2)設函數f(x)=ax(a>0,且a≠1)的圖象與y=x的圖象有公共點,證明:f(x)=ax∈M;
(3)若函數f(x)=sinkx∈M,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠的一臺某型號機器有2種工作狀態:正常狀態和故障狀態.若機器處于故障狀態,則停機檢修.為了檢查機器工作狀態是否正常,工廠隨機統計了該機器以往正常工作狀態下生產的1000個產品的質量指標值,得出如圖1所示頻率分布直方圖.由統計結果可以認為,這種產品的質量指標值服從正態分布![]() ,其中
,其中![]() 近似為這1000個產品的質量指標值的平均數
近似為這1000個產品的質量指標值的平均數![]() ,
,![]() 近似為這1000個產品的質量指標值的方差
近似為這1000個產品的質量指標值的方差![]() (同一組中的數據用該組區間中點值為代表).若產品的質量指標值全部在
(同一組中的數據用該組區間中點值為代表).若產品的質量指標值全部在![]() 之內,就認為機器處于正常狀態,否則,認為機器處于故障狀態.
之內,就認為機器處于正常狀態,否則,認為機器處于故障狀態.
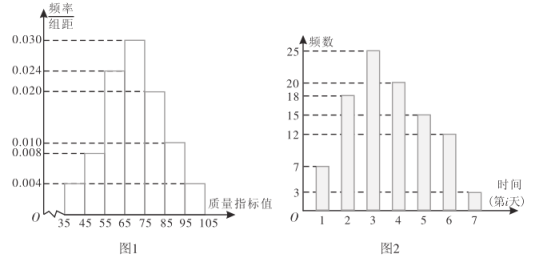
(1)下面是檢驗員在一天內從該機器生產的產品中隨機抽取10件測得的質量指標值:
29 45 55 63 67 73 78 87 93 113
請判斷該機器是否出現故障?
(2)若機器出現故障,有2種檢修方案可供選擇:
方案一:加急檢修,檢修公司會在當天排除故障,費用為700元;
方案二:常規檢修,檢修公司會在七天內的任意一天來排除故障,費用為200元.
現需決策在機器出現故障時,該工廠選擇何種方案進行檢修,為此搜集檢修公司對該型號機器近100單常規檢修在第i(![]() ,2,…,7)天檢修的單數,得到如圖2所示柱狀圖,將第i天常規檢修單數的頻率代替概率.已知該機器正常工作一天可收益200元,故障機器檢修當天不工作,若機器出現故障,該選擇哪種檢修方案?
,2,…,7)天檢修的單數,得到如圖2所示柱狀圖,將第i天常規檢修單數的頻率代替概率.已知該機器正常工作一天可收益200元,故障機器檢修當天不工作,若機器出現故障,該選擇哪種檢修方案?
附:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
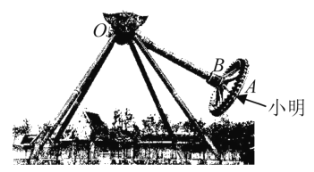
【題目】如圖,大擺錘是一種大型的游樂設備,常見于各大游樂園.游客坐在圓形的座艙中,面向外.通常,大擺錘以壓肩作為安全束縛,配以安全帶作為二次保險.座艙旋轉的同時,懸掛座艙的主軸在電機的驅動下做單擺運動.大擺錘的運行可以使置身其上的游客驚心動魄.今年元旦,小明去某游樂園玩“大擺錘”,他坐在點![]() 處,“大擺錘”啟動后,主軸
處,“大擺錘”啟動后,主軸![]() 在平面
在平面![]() 內繞點
內繞點![]() 左右擺動,平面
左右擺動,平面![]() 與水平地面垂直,
與水平地面垂直,![]() 擺動的過程中,點
擺動的過程中,點![]() 在平面
在平面![]() 內繞點
內繞點![]() 作圓周運動,并且始終保持
作圓周運動,并且始終保持![]() ,
,![]() ,已知
,已知![]() ,在“大擺錘”啟動后,下列
,在“大擺錘”啟動后,下列![]() 個結論中正確的是______(請填上所有正確結論的序號).
個結論中正確的是______(請填上所有正確結論的序號).
①點![]() 在某個定球面上運動;
在某個定球面上運動;
②線段![]() 在水平地面上的正投影的長度為定值;
在水平地面上的正投影的長度為定值;
③直線![]() 與平面
與平面![]() 所成角的正弦值的最大值為
所成角的正弦值的最大值為![]() ;
;
④直線![]() 與平面
與平面![]() 所成角的正弦值的最大值為
所成角的正弦值的最大值為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱柱![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點,
的中點,![]() .
.
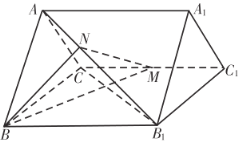
(1)求證:![]() 平面
平面![]() ;
;
(2)條件①:直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ;
;
條件②:![]() 為銳角,三棱錐
為銳角,三棱錐![]() 的體積為
的體積為![]() .
.
在以上兩個條件中任選一個,補充在下面的問題中,并解決該問題:
若平面![]() 平面
平面![]() ,______,求平面
,______,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為
為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為![]() .
.
(1)求曲線C的極坐標方程和直線l的直角坐標方程;
(2)若射線![]() 與曲線C交于點A(不同于極點O),與直線l交于點B,求
與曲線C交于點A(不同于極點O),與直線l交于點B,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,正四棱錐![]() 底面的四個頂點
底面的四個頂點![]() ,
,![]() ,
,![]() ,
,![]() 在球
在球![]() 的同一個大圓上,點
的同一個大圓上,點![]() 在球面上,且已知
在球面上,且已知![]() .
.
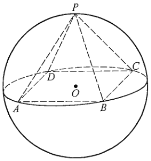
(1)求球![]() 的表面積;
的表面積;
(2)設![]() 為
為![]() 中點,求異面直線
中點,求異面直線![]() 與
與![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com