奇函數 偶函數 即是奇函數又是偶函數 非奇非偶函數
分析:(I)先判斷f(x)=x
5+5x的定義域是否關于原點對稱,再判斷f(-x)與f(x)的關系,根據奇函數的定義可得結論;
(II)先判斷f(x)=x
4+2x
2-1的定義域是否關于原點對稱,再判斷f(-x)與f(x)的關系,根據偶函數的定義可得結論;
(III)先判斷y=
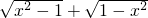
的定義域是否關于原點對稱,再判斷f(-x)與f(x)的關系,根據奇函數和偶函數的定義可得結論;
(IV)根據f(x)=2x
2-1,x∈[-2,3]的定義域不關于原點對稱,可得結論;
解答:(Ⅰ)f(x)=x
5+5x的定義域R關于原點對稱
且f(x)=-x
5-5x=-f(x)
故f(x)=x
5+5x為奇函數
(Ⅱ)f(x)=x
4+2x
2-1的定義域R關于原點對稱;
且f(-x)=x
4+2x
2-1=f(x)
故函數f(x)=x
4+2x
2-1為偶函數
(Ⅲ)y=
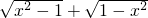
的定義域{-1,1}關于原點對稱;
且f(-1)=f(1)=0
即f(-x)=f(x)且f(-x)=-f(x)
故函數y=
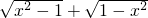
即是奇函數又是偶函數
(Ⅳ)f(x)=2x
2-1,x∈[-2,3]的定義域不關于原點對稱;
故函數f(x)=2x
2-1,x∈[-2,3]是非奇非偶函數
故答案為:奇函數,偶函數,即是奇函數又是偶函數,非奇非偶函數
點評:本題考查的知識點是函數奇偶性的判斷,熟練掌握函數奇偶性的判斷方法是解答的關鍵.

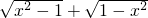 ;________
;________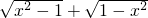 的定義域是否關于原點對稱,再判斷f(-x)與f(x)的關系,根據奇函數和偶函數的定義可得結論;
的定義域是否關于原點對稱,再判斷f(-x)與f(x)的關系,根據奇函數和偶函數的定義可得結論;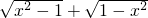 的定義域{-1,1}關于原點對稱;
的定義域{-1,1}關于原點對稱; 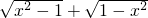 即是奇函數又是偶函數
即是奇函數又是偶函數

 名校課堂系列答案
名校課堂系列答案