
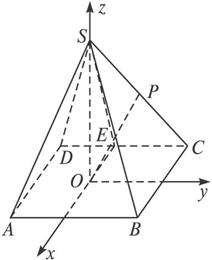
(1)求證:![]() 是定值.
是定值.
(2)已知P是SC的中點,且SO=3,問在棱SA上是否存在一點Q,使異面直線OP與BQ所成的角為90°?若存在,請給出證明,并求出AQ的長;若不存在,請說明理由.
(文)如圖,在四棱錐S—ABCD中,底面ABCD是正方形,SA⊥平面ABCD,且SA=AB,點E為AB的中點,點F為SC的中點.
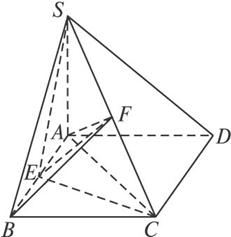
(1)求證:EF⊥CD;
(2)求證:平面SCD⊥平面SCE.
(理)(1)證明:在△SDC內,作SE⊥CD交CD于E,連結OE.

∵SO⊥平面ABCD,∴SO⊥CD.
∴CD⊥平面SOE.
∴CD⊥OE.
∴OE∥AD.
∴DE=1,從而CE=3.
![]() cos∠SCD=
cos∠SCD=![]() =12,
=12,
∴![]() 是定值.
是定值.
(2)解:以O為坐標原點,以OS所在直線為Oz軸,以過O且平行于AD的直線為Ox軸,以過O且平行于AB的直線為Oy軸,建立如圖所示的空間直角坐標系.
于是,A(2,-1,0)、B(2,3,0)、C(-2,3,0)、S(0,0,3)、P(-1,![]() ).
).
設點Q(x,y,z),則存在λ使![]() (這是關鍵!將點的坐標用一個變量表示),
(這是關鍵!將點的坐標用一個變量表示),
即(x-2,y+1,z)=λ(-2,1,3),
得 即
即
令![]() =(-1,
=(-1,![]() )·(-2λ,λ-4,3λ)=8λ-6=0,得λ=
)·(-2λ,λ-4,3λ)=8λ-6=0,得λ=![]() .
.
由0<λ<1,知點Q在棱SA上,且Q(![]() ),
),![]() .
.
(文)證明:(1)如圖,連結AC、AF、BF、EF,

∵SA⊥平面ABCD,
∴AF為Rt△SAC斜邊SC上的中線.
∴AF=![]() SC.
SC.
又∵ABCD是正方形,
∴CB⊥AB.
而由SA⊥平面ABCD,得CB⊥SA.
∴CB⊥平面SAB.
∴CB⊥SB.
∴BF為Rt△SBC斜邊SC上的中線.
∴BF=![]() SC.
SC.
∴△AFB為等腰三角形,EF⊥AB.
又CD∥AB,
∴EF⊥CD.
(2)由已知易得Rt△SAE≌Rt△CBE,
∴SE=EC,即△SEC是等腰三角形.
∴EF⊥SC.
又∵SC∩CD=C,∴EF⊥平面SCD.
又EF![]() 平面SCE,
平面SCE,
∴平面SCD⊥平面SCE.


科目:高中數學 來源: 題型:
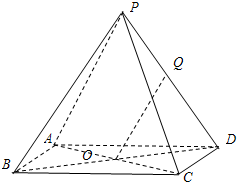 (2007•靜安區一模)(理) 如圖,已知四棱錐P-ABCD的底面ABCD是邊長為a的正方形,點O為該正方形的中心,側棱PA=PC,PB=PD.
(2007•靜安區一模)(理) 如圖,已知四棱錐P-ABCD的底面ABCD是邊長為a的正方形,點O為該正方形的中心,側棱PA=PC,PB=PD.查看答案和解析>>
科目:高中數學 來源: 題型:
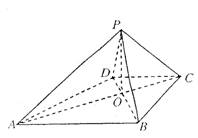
(08年濱州市質檢三理) 如圖,已知四棱錐P―ABCD的底面ABCD為等腰三角梯形,AB∥CD,AC⊥BC,AC∩BD=0,且頂點P在底面上的射影恰為O點,又OB=2,OP=![]() ,PD⊥PD.
,PD⊥PD.
(1)求二面角B―PA―D的余弦的絕對值;
(2)在棱PC上是否存在點M,使PC⊥平面BMD?若存在,求出點M的位置;若不存在,試說明理由。
(3)在(2)的條件下,求三棱錐C―BMD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
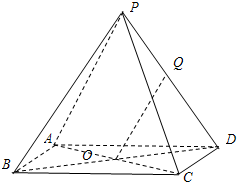 (理) 如圖,已知四棱錐P-ABCD的底面ABCD是邊長為a的正方形,點O為該正方形的中心,側棱PA=PC,PB=PD.
(理) 如圖,已知四棱錐P-ABCD的底面ABCD是邊長為a的正方形,點O為該正方形的中心,側棱PA=PC,PB=PD.查看答案和解析>>
科目:高中數學 來源:2008年上海市靜安區高考數學一模試卷(文理合卷)(解析版) 題型:解答題
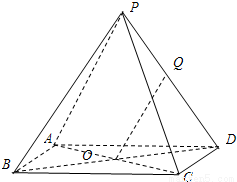
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com