
【題目】已知函數![]()
(Ⅰ)若![]() ,求證:函數
,求證:函數![]() 在(1,+∞)上是增函數;
在(1,+∞)上是增函數;
(Ⅱ)求函數![]() 在[1,e]上的最小值及相應的
在[1,e]上的最小值及相應的![]() 值.
值.
【答案】(Ⅰ)函數f(x)在(1,+∞)上是增函數;(Ⅱ)見解析.
【解析】試題分析:(Ⅰ)代入![]() ,求導,通過導數恒為正值進行證明;(Ⅱ)求導,通過討論參數的取值,研究函數的極值點與所給區間的關系,進而研究函數在所給區間上的單調性和極值、最值進行求解.
,求導,通過導數恒為正值進行證明;(Ⅱ)求導,通過討論參數的取值,研究函數的極值點與所給區間的關系,進而研究函數在所給區間上的單調性和極值、最值進行求解.
試題解析:(Ⅰ)當a=﹣2時,f(x)=x2﹣2lnx,當x∈(1,+∞),![]() ,故函數f(x)在(1,+∞)上是增函數.
,故函數f(x)在(1,+∞)上是增函數.
(Ⅱ)![]() ,當x∈[1,e],2x2+a∈[a+2,a+2e2].
,當x∈[1,e],2x2+a∈[a+2,a+2e2].
若a≥﹣2,f'(x)在[1,e]上非負(僅當a=﹣2,x=1時,f'(x)=0),
故函數f(x)在[1,e]上是增函數,此時[f(x)]min=f(1)=1.
若﹣2e2<a<﹣2,當![]() 時,f'(x)=0;當
時,f'(x)=0;當![]() 時,f'(x)<0,
時,f'(x)<0,
此時f(x)是減函數;當![]() 時,f'(x)>0,此時f(x)是增函數.
時,f'(x)>0,此時f(x)是增函數.
故[f(x)]min= =
=![]()
若a≤﹣2e2,f'(x)在[1,e]上非正(僅當a=﹣2e2,x=e時,f'(x)=0),
故函數f(x)在[1,e]上是減函數,此時[f(x)]min=f(e)=a+e2.
綜上可知,當a≥﹣2時,f(x)的最小值為1,相應的x值為1;
當﹣2e2<a<﹣2時,f(x)的最小值為![]() ,相應的x值為
,相應的x值為![]() ;
;
當a≤﹣2e2時,f(x)的最小值為a+e2,相應的x值為e


科目:高中數學 來源: 題型:
【題目】某氣象儀器研究所按以下方案測試一種“彈射型”氣象觀測儀器的垂直彈射高度:A、B、C三地位于同一水平面上,在C處進行該儀器的垂直彈射,觀測點A、B兩地相距100米,∠BAC=60°,在A地聽到彈射聲音的時間比在B地晚![]()
秒. A地測得該儀器彈至最高點H時的仰角為30°.
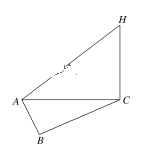
(1)求A、C兩地的距離;
(2)求該儀器的垂直彈射高度CH.(聲音的傳播速度為340米/秒)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐V-ABC中,平面VAB![]() 平面ABC,
平面ABC, ![]() VAB為等邊三角形,AC
VAB為等邊三角形,AC![]() BC且AC=BC=
BC且AC=BC=![]() ,O,M分別為AB,VA的中點。
,O,M分別為AB,VA的中點。
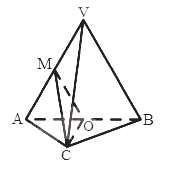
(I)求證:VB//平面MOC;
(II)求證:平面MOC![]() 平面VAB;
平面VAB;
(III)求三棱錐V-ABC的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若直線![]() 和
和![]() 是異面直線,
是異面直線,![]() 在平面
在平面![]() 內,
內,![]() 在平面
在平面![]() 內,
內,![]() 是平面
是平面![]() 與平面
與平面![]() 的交線,則下列結論正確的是( )
的交線,則下列結論正確的是( )
A. ![]() 至少與
至少與![]() ,
,![]() 中的一條相交 B.
中的一條相交 B. ![]() 與
與![]() ,
,![]() 都不相交
都不相交
C. ![]() 與
與![]() ,
,![]() 都相交 D.
都相交 D. ![]() 至多與
至多與![]() ,
,![]() 中的一條相交
中的一條相交
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com