【題目】有一座大橋既是交通擁擠地段，又是事故多發地段，為了保證安全，交通部門規定：大橋上的車距d（m）與車速v（km/h）和車身長l（m）的關系滿足：d=kv2l+ 
l（k為正的常數），假定大橋上的車的車身長都為4m，當車速為60km/h時，車距為2.66個車身長．
（1）寫出車距d關于車速v的函數關系式；
（2）應規定怎樣的車速，才能使大橋上每小時通過的車輛最多？
【答案】
（1）解：因為當v=60時，d=2.66l，所以 
，
∴d=0.0024v2+2
（2）解：設每小時通過的車輛為Q，每小時內通過汽車的數量為Q最大，只須 
最小，
即Q= 
∵ 
，
當且僅當 
，即v=50時，Q取最大值 
．
答：當v=50（km/h）時，大橋每小時通過的車輛最多
【解析】（1）根據當車速為60（km/h）時，車距為2.66個車身長，建立等式關系，求出k的值，即可求出車距d關于車速v的函數關系式；（2）設每小時通過的車輛為Q，每小時內通過汽車的數量為Q最大，只須 最小，將d代入，然后利用基本不等式求出最值，即可求出所求．
【考點精析】解答此題的關鍵在于理解基本不等式的相關知識，掌握基本不等式：
,（當且僅當
時取到等號）；變形公式：
．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
，g（x）=f（x）﹣a
（1）當a=2時，求函數g（x）的零點；
（2）若函數g（x）有四個零點，求a的取值范圍；
（3）在（2）的條件下，記g（x）得四個零點分別為x1 ， x2 ， x3 ， x4 ， 求x1+x2+x3+x4的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，內角A、B、C所對的邊分別是a、b、c，且a+b+c=8． （Ⅰ）若a=2，b= 
，求cosC的值；
（Ⅱ）若sinAcos2 
+sinBcos2 
=2sinC，且△ABC的面積S= 
sinC，求a和b的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】袋中有質地、大小完全相同的5個小球，編號分別為1，2，3，4，5，甲、乙兩人玩一種游戲．甲先摸出一個球．記下編號，放回后再摸出一個球，記下編號，如果兩個編號之和為偶數．則算甲贏，否則算乙贏．
（1）求甲贏且編號之和為6的事件發生的概率：
（2）試問：這種游戲規則公平嗎．請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】根據題意解答
（1）利用“五點法”畫出函數 
在長度為一個周期的閉區間的簡圖．
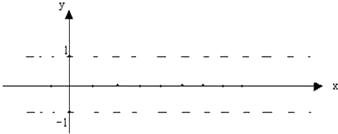
（2）并說明該函數圖像可由y=sinx（x∈R）的圖像經過怎樣平移和伸縮變換得到的．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校為緩解高三學生的高考壓力，經常舉行一些心理素質綜合能力訓練活動，經過一段時間的訓練后從該年級800名學生中隨機抽取100名學生進行測試，并將其成績分為
、
、
、
、
五個等級，統計數據如圖所示（視頻率為概率），根據以上抽樣調查數據，回答下列問題：
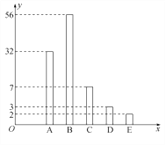
（1）試估算該校高三年級學生獲得成績為
的人數；
（2）若等級
、
、
、
、
分別對應100分、90分、80分、70分、60分，學校要求平均分達90分以上為“考前心理穩定整體過關”，請問該校高三年級目前學生的“考前心理穩定整體”是否過關？
（3）為了解心理健康狀態穩定學生的特點，現從
、
兩種級別中，用分層抽樣的方法抽取11個學生樣本，再從中任意選取3個學生樣本分析，求這3個樣本為
級的個數
的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
