
在 中,已知
中,已知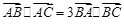 .
.
(1)求證: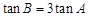 ;
;
(2)若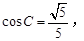 求角A的大小.
求角A的大小.
(1)證明見解析;(2) .
.
【解析】
試題分析:(1)已知的向量的數(shù)量積,要證明的是角的關(guān)系,故我們首先運(yùn)用數(shù)量積定義把已知轉(zhuǎn)化為三角形的邊角關(guān)系,由已知可得 ,即
,即 ,考慮到求證式只是角的關(guān)系,因此我們再應(yīng)用正弦定理把式子中邊的關(guān)系轉(zhuǎn)化為角的關(guān)系,即有
,考慮到求證式只是角的關(guān)系,因此我們再應(yīng)用正弦定理把式子中邊的關(guān)系轉(zhuǎn)化為角的關(guān)系,即有 ,而這時(shí)兩邊同除以
,而這時(shí)兩邊同除以 即得待證式(要說明
即得待證式(要說明 均不為零).(2)要求解
均不為零).(2)要求解 的大小,一般是求出這個角的某個三角函數(shù)值,本題應(yīng)該求
的大小,一般是求出這個角的某個三角函數(shù)值,本題應(yīng)該求 ,因?yàn)椋?)中有
,因?yàn)椋?)中有 可利用,思路是
可利用,思路是 .
.
試題解析:(1)∵ ,∴
,∴ ,
,
即 .
2分
.
2分
由正弦定理,得 ,∴
,∴ .
4分
.
4分
又∵ ,∴
,∴ .∴
.∴ 即
即 . 6分
. 6分
(2)∵  ,∴
,∴ .∴
.∴ .8分
.8分
∴ ,即
,即 .∴
.∴ .
10分
.
10分
由 (1) ,得 ,解得
,解得 . 12分
. 12分
∵ ,∴
,∴ .∴
.∴ . 14分
. 14分
考點(diǎn):(1)向量的數(shù)量積的定義與正弦定理;(2)已知三角函數(shù)值,求角.


 科學(xué)實(shí)驗(yàn)活動冊系列答案
科學(xué)實(shí)驗(yàn)活動冊系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年江蘇省蘇北四市(徐、連、淮、宿)高三元月調(diào)研測試數(shù)學(xué)試卷 題型:填空題
在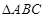 中,已知BC=1,B=
中,已知BC=1,B=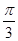 ,則
,則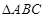 的面積為
的面積為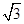 ,則AC和長為 ▲
,則AC和長為 ▲
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年河南省高二年級月考數(shù)學(xué)試題 題型:解答題
在 中,已知
中,已知 ,
, .(15分)
.(15分)
(1)若 ,求
,求 ;
;
(2)求 的最大角的弧度數(shù).
的最大角的弧度數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆湖北省高一第二學(xué)期期中考試?yán)砜茢?shù)學(xué)卷 題型:解答題
在 中,已知
中,已知 ,
, .
.
(1)若 ,求
,求 ;
;
(2)求 的最大角的弧度數(shù).
的最大角的弧度數(shù).
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com