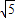已知實數x,y滿足關系:x2+y2-2x+4y-20=0,則x2+y2的最小值 .
【答案】
分析:把圓的方程化為標準方程后,找出圓心坐標和圓的半徑r,設圓上一點的坐標為(x,y),原點坐標為(0,0),則x
2+y
2表示圓上一點和原點之間的距離的平方,根據圖象可知此距離的最小值為圓的半徑r減去圓心到原點的距離,利用兩點間的距離公式求出圓心到原點的距離,利用半徑減去求出的距離,然后平方即為x
2+y
2的最小值.
解答: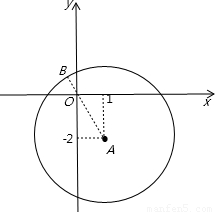
解:把圓的方程化為標準方程得:
(x-1)
2+(y+2)
2=25,則圓心A坐標為(1,-2),圓的半徑r=5,
設圓上一點的坐標為(x,y),原點O坐標為(0,0),
則|AO|=
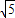
,|AB|=r=5,
所以|BO|=|AB|-|OA|=5-
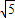
.
則x
2+y
2的最小值為
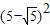
=30-10
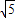
.
故答案為:30-10
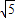 點評:
點評:此題考查學生會把圓的一般方程化為圓的標準方程并會由圓的標準方程找出圓心坐標與半徑,考查了數形結合的數學思想,是一道中檔題.

 解:把圓的方程化為標準方程得:
解:把圓的方程化為標準方程得: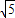 ,|AB|=r=5,
,|AB|=r=5,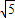 .
.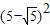 =30-10
=30-10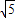 .
.