
��֪�E�A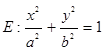 ��a��b��0�����x���ʞ�
��a��b��0�����x���ʞ�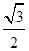 �����^(gu��)�c(di��n)��
�����^(gu��)�c(di��n)��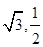 ����
����
��1����E�AE�ķ��̣�
��2���O(sh��)ֱ��l:y=kx+t�c�A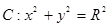 ��1��R��2���������c(di��n)A����l�c�E�AEֻ��һ��(g��)�����c(di��n)B.
��1��R��2���������c(di��n)A����l�c�E�AEֻ��һ��(g��)�����c(di��n)B.
�����C��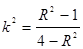 ��
��
�ڮ�(d��ng)R���ֵ�r(sh��)��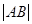 ȡ�����ֵ����������ֵ��
ȡ�����ֵ����������ֵ��
(1)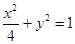 ����2�����C��Ҋ(ji��n)��������
����2�����C��Ҋ(ji��n)��������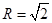 �r(sh��)��
�r(sh��)��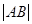 ȡ�����ֵ��1��
ȡ�����ֵ��1��
����ԇ�}������(1)�E�A���x���ʞ�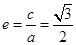 ���֙E�A�^(gu��)��֪�c(di��n)����
���֙E�A�^(gu��)��֪�c(di��n)����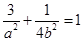 ���ټ���
���ټ���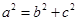 ��(li��n)�������
��(li��n)������� ����2��ֱ���c�A���E�A�����У���˿���ֱ�������c�E�A����(��A����)(li��n)�����̽M���˷��̽Mֻ��һ�⣬�ɴ˿ɵõ��}�Ѕ���(sh��)���P(gu��n)ϵʽ����(d��ng)Ȼֱ���c�A���У������ÈA�ĵ�ֱ���ľ��x���ڈA�İ돽��(l��i)��ʽ���õ��ăɂ�(g��)��ʽ����ȥ����(sh��)
����2��ֱ���c�A���E�A�����У���˿���ֱ�������c�E�A����(��A����)(li��n)�����̽M���˷��̽Mֻ��һ�⣬�ɴ˿ɵõ��}�Ѕ���(sh��)���P(gu��n)ϵʽ����(d��ng)Ȼֱ���c�A���У������ÈA�ĵ�ֱ���ľ��x���ڈA�İ돽��(l��i)��ʽ���õ��ăɂ�(g��)��ʽ����ȥ����(sh��)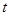 �����C�â�ʽ������Ҫ��
�����C�â�ʽ������Ҫ��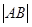 �����ֵ���������
�����ֵ���������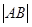 ��ע�
��ע�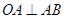 �����
�����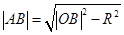 ���@���O(sh��)
���@���O(sh��)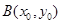 ���ɢ��еķ���(�M)�����
���ɢ��еķ���(�M)�����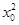 ����K��
����K��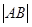 ��
��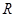 ��ʾ��
��ʾ��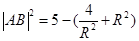 �����ò���ʽ֪�R(sh��)�Ϳ�������ֵ.
�����ò���ʽ֪�R(sh��)�Ϳ�������ֵ.
ԇ�}������(1)�E�AE�ķ��̞�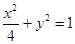 4��
4��
��2������?y��n)�ֱ�� �c�AC:
�c�AC: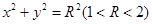 ������A,��
������A,��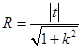 ,
,
�� �� 5��
�� 5��
����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/aa/c/hm5rs3.png" style="vertical-align:middle;" />�c�E�AEֻ��һ��(g��)�����c(di��n)B��
��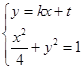 ��
��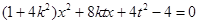 ,�Ҵ˷�����Ψһ��.
,�Ҵ˷�����Ψһ��.
�t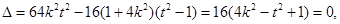 ��
��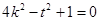
���ɢ٢�,��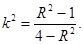 8��
8��
���O(sh��) ����
����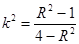 ��
��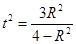
���f�_(d��)����,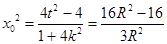
��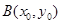 �c(di��n)�ڙE�A��,��
�c(di��n)�ڙE�A��,��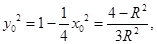
��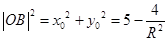 10��
10��
��ֱ��������OAB��,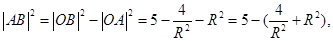
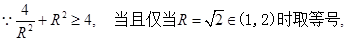
�� 12��
12��
���c(di��n)���E�A�Ę�(bi��o)��(zh��n)���̣�ֱ���c�A���У�ֱ���c�E�A����.


 �߲��}�����㑪(y��ng)��һ�c(di��n)ͨϵ�д�
�߲��}�����㑪(y��ng)��һ�c(di��n)ͨϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�o���E�A ���Q�A����ԭ�c(di��n)O���돽��
���Q�A����ԭ�c(di��n)O���돽�� �ĈA�ǙE�AC�ġ���(zh��n)�A�������E�AC��һ��(g��)���c(di��n)��
�ĈA�ǙE�AC�ġ���(zh��n)�A�������E�AC��һ��(g��)���c(di��n)��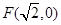 ������S�ϵ�һ��(g��)���c(di��n)��F�ľ��x��
������S�ϵ�һ��(g��)���c(di��n)��F�ľ��x��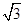 ��
��
(1)��E�AC�ķ��̺��䡰��(zh��n)�A�����̣�
(2)�c(di��n)P�ǙE�AC�ġ���(zh��n)�A���ϵ�һ��(g��)��(d��ng)�c(di��n)���^(gu��)��(d��ng)�c(di��n)P��ֱ��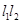 ��ʹ��
��ʹ��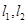 �c�E�AC��ֻ��һ��(g��)���c(di��n)��ԇ�Д�
�c�E�AC��ֻ��һ��(g��)���c(di��n)��ԇ�Д�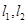 �Ƿ�ֱ�����f(shu��)�����ɣ�
�Ƿ�ֱ�����f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D����֪�E�A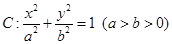 �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe�� ��������c(di��n)��
��������c(di��n)�� ��֪
��֪ ��߅�L(zh��ng)��
��߅�L(zh��ng)�� ���������Σ�
����������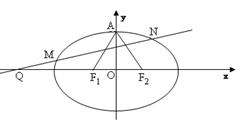
��1����E�A �ķ��̣�
�ķ��̣�
��2���^(gu��)�c(di��n)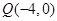 ����һ��(d��ng)ֱ��
����һ��(d��ng)ֱ�� ���E�A
���E�A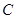 ��
��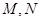 ���c(di��n)��ӛ
���c(di��n)��ӛ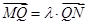 �����ھ���
�����ھ���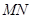 ��ȡһ�c(di��n)
��ȡһ�c(di��n) ��ʹ��
��ʹ��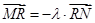 ����(d��ng)ֱ��
����(d��ng)ֱ�� �\(y��n)��(d��ng)�r(sh��)���c(di��n)
�\(y��n)��(d��ng)�r(sh��)���c(di��n) ��ijһ��ֱ�����\(y��n)��(d��ng)�����ԓ��ֱ���ķ��̣�
��ijһ��ֱ�����\(y��n)��(d��ng)�����ԓ��ֱ���ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�AC��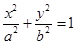 ��a>b>0�����^(gu��)�c(di��n)(0��1)�����x���ʞ�
��a>b>0�����^(gu��)�c(di��n)(0��1)�����x���ʞ�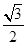 ��
��
(1)��E�AC�ķ��̣�
(2)A��B��E�AC��������c(di��n)��ֱ��l��x=2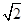 �cx�S�����c(di��n)D���c(di��n)P�ǙE�AC�Ϯ���A��B�Ą�(d��ng)�c(di��n)��ֱ��AP��BP�քe��ֱ��l��E��F(xi��n)���c(di��n)���C������(d��ng)�c(di��n)P�ڙE�AC���\(y��n)��(d��ng)�r(sh��)��
�cx�S�����c(di��n)D���c(di��n)P�ǙE�AC�Ϯ���A��B�Ą�(d��ng)�c(di��n)��ֱ��AP��BP�քe��ֱ��l��E��F(xi��n)���c(di��n)���C������(d��ng)�c(di��n)P�ڙE�AC���\(y��n)��(d��ng)�r(sh��)�� ��鶨ֵ��
��鶨ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D����֪ƽ���(n��i)һ��(d��ng)�c(di��n)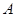 ���ɂ�(g��)���c(di��n)
���ɂ�(g��)���c(di��n) ��
��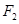 �ľ��x֮�͞�
�ľ��x֮�͞�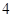 ������
������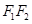 ���L(zh��ng)��
���L(zh��ng)��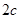
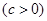 .
.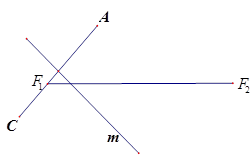
��1�����(d��ng)�c(di��n) ��܉�E
��܉�E ��
��
��2����(d��ng) �r(sh��)���^(gu��)�c(di��n)
�r(sh��)���^(gu��)�c(di��n) ��ֱ��
��ֱ�� �c܉�E
�c܉�E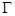 ����
����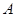 ��
�� ���c(di��n)�����c(di��n)
���c(di��n)�����c(di��n)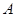 �ھ���
�ھ���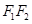 ���Ϸ�������
���Ϸ�������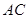 �Ĵ�ֱƽ�־���
�Ĵ�ֱƽ�־���
����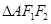 ����e�����ֵ��
����e�����ֵ��
��܉�E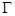 ���Ƿ���ڳ�
���Ƿ���ڳ�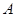 ��
�� ���c(di��n)
���c(di��n)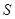 ��
��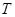 �P(gu��n)��ֱ��
�P(gu��n)��ֱ�� ��(du��)�Q��Ո(q��ng)�f(shu��)������.
��(du��)�Q��Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�c(di��n)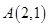 �ڒ��タ
�ڒ��タ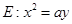 �ϣ�ֱ��
�ϣ�ֱ��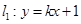 ��
�� ����
����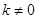 ���c���タ
���c���タ ���ཻ��
���ཻ��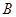 ��
�� ���c(di��n)��ֱ��
���c(di��n)��ֱ�� ��
�� �քe��ֱ��
�քe��ֱ��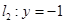 ���c(di��n)
���c(di��n) ��
��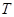 .
.
��1����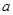 ��ֵ��
��ֵ��
��2����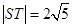 ����ֱ��
����ֱ�� �ķ��̣�
�ķ��̣�
��3��ԇ�Д��Ծ���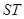 ��ֱ���ĈA�Ƿ���^(gu��)�ɂ�(g��)���c(di��n)�����ǣ����@�ɂ�(g��)���c(di��n)������(bi��o)�������ǣ��f(shu��)������.
��ֱ���ĈA�Ƿ���^(gu��)�ɂ�(g��)���c(di��n)�����ǣ����@�ɂ�(g��)���c(di��n)������(bi��o)�������ǣ��f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪���タ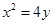 ��ֱ��
��ֱ��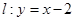 ��
��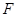 �ǒ��タ�Ľ��c(di��n)��
�ǒ��タ�Ľ��c(di��n)��
��1���ڒ��タ����һ�c(di��n) ��ʹ�c(di��n)
��ʹ�c(di��n) ��ֱ��
��ֱ�� �ľ��x��С��
�ľ��x��С��
(2)��D���^(gu��)�c(di��n)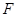 ��ֱ�������タ��A��B���c(di��n).
��ֱ�������タ��A��B���c(di��n).
����ֱ��AB�ăAб�Ǟ�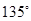 ������AB���L(zh��ng)�ȣ�
������AB���L(zh��ng)�ȣ�
����ֱ��AO��BO�քe��ֱ�� ��
��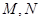 ���c(di��n),��
���c(di��n),��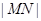 ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵxOy�У��O(sh��)����C1�� �����ɵķ��]�D�ε���e��
�����ɵķ��]�D�ε���e�� ������C1�ϵ��c(di��n)��ԭ�c(di��n)O����̾��x��
������C1�ϵ��c(di��n)��ԭ�c(di��n)O����̾��x�� ��������C1�c����(bi��o)�S�Ľ��c(di��n)����c(di��n)�ęE�Aӛ��C2��
��������C1�c����(bi��o)�S�Ľ��c(di��n)����c(di��n)�ęE�Aӛ��C2��
��1����E�AC2�Ę�(bi��o)��(zh��n)���̣�
��2���O(sh��)AB���^(gu��)�E�AC2����O�������ң�l�Ǿ���AB�Ĵ�ֱƽ�־���M��l�ϵ��c(di��n)���cO���غϣ���
����MO��2OA����(d��ng)�c(di��n)A�ڙE�AC2���\(y��n)��(d��ng)�r(sh��)�����c(di��n)M��܉�E���̣�
����M��l�c�E�AC2�Ľ��c(di��n)�����AMB����e����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�A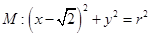
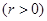 ,���E�A
,���E�A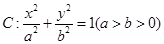 ������c(di��n)��A
������c(di��n)��A �ĈA�ģ��x���ʞ�
�ĈA�ģ��x���ʞ�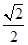 ��
��
��1����E�AC�ķ��̣�
��2��������ֱ��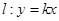 ��ʹ��ֱ��
��ʹ��ֱ�� �c�E�A
�c�E�A �քe����
�քe����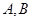 ���c(di��n)���c�A
���c(di��n)���c�A �քe����
�քe����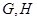 ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)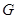 �ھ���
�ھ���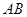 �ϣ���
�ϣ���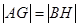 ����A
����A �İ돽
�İ돽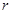 ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com