
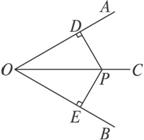
圖
 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
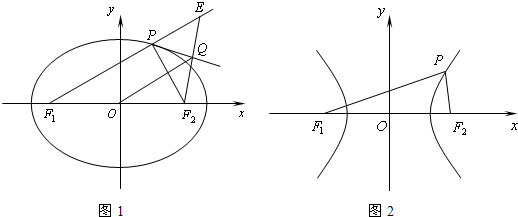
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 1 |
| kk1 |
| 1 |
| kk2 |
查看答案和解析>>
科目:高中數學 來源:2013年普通高等學校招生全國統一考試(山東卷)、理科數學 題型:044
橢圓C:![]() 的左、右焦點分別是F1.F2,離心率為
的左、右焦點分別是F1.F2,離心率為![]() 過F,且垂直于x軸的直線被橢圓C截得的線段長為l.
過F,且垂直于x軸的直線被橢圓C截得的線段長為l.
(Ⅰ)求橢圓C的方程;
(Ⅱ)點P是橢圓C上除長軸端點外的任一點,連接PF1,PF2,設∠F1PF2的角平分線PM交C的長軸于點M(m,0),求m的取值范圍;
(Ⅲ)在(Ⅱ)的條件下,過點p作斜率為k的直線l,使得l與橢圓C有且只有一個公共點.
設直線PF1,PF2的斜率分別為k1,k2,若k≠0,試證明![]() 為定值,并求出這個定值.
為定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源:2013年全國普通高等學校招生統一考試理科數學(山東卷解析版) 題型:解答題
橢圓 :
: 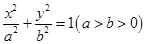 的左、右焦點分別是
的左、右焦點分別是 ,離心率為
,離心率為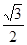 ,過
,過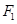 且垂直于
且垂直于 軸的直線被橢圓
軸的直線被橢圓 截得的線段長為
截得的線段長為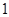 。
。
(Ⅰ)求橢圓 的方程;
的方程;
(Ⅱ)點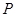 是橢圓
是橢圓 上除長軸端點外的任一點,連接
上除長軸端點外的任一點,連接 ,設
,設 的角平分線
的角平分線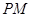 交
交 的長軸于點
的長軸于點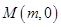 ,求
,求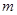 的取值范圍;
的取值范圍;
(Ⅲ)在(Ⅱ)的條件下,過點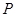 作斜率為
作斜率為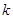 的直線
的直線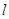 ,使
,使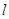 與橢圓
與橢圓 有且只有一個公共點,設直線的
有且只有一個公共點,設直線的 斜率分別為
斜率分別為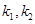 。若
。若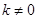 ,試證明
,試證明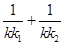 為定值,并求出這個定值。
為定值,并求出這個定值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com