
【題目】如圖,在平面直角坐標系xOy中,一單位圓的圓心的初始位置在(0,1),此時圓上一點P的位置在(0,0),圓在x軸上沿正向滾動.當圓滾動到圓心位于(2,1)時, ![]() 的坐標為 .
的坐標為 . 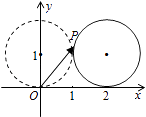
【答案】(2﹣sin2,1﹣cos2)
【解析】解:設滾動后的圓的圓心為O',切點為A(2,0),連接O'P,
過O'作與x軸正方向平行的射線,交圓O'于B(3,1),設∠BO'P=θ
∵⊙O'的方程為(x﹣2)2+(y﹣1)2=1,
∴根據圓的參數方程,得P的坐標為(2+cosθ,1+sinθ),
∵單位圓的圓心的初始位置在(0,1),圓滾動到圓心位于(2,1)
∴∠AO'P=2,可得θ= ![]() ﹣2
﹣2
可得cosθ=cos( ![]() ﹣2)=﹣sin2,sinθ=sin(
﹣2)=﹣sin2,sinθ=sin( ![]() ﹣2)=﹣cos2,
﹣2)=﹣cos2,
代入上面所得的式子,得到P的坐標為(2﹣sin2,1﹣cos2)
∴ ![]() 的坐標為(2﹣sin2,1﹣cos2).
的坐標為(2﹣sin2,1﹣cos2).
所以答案是:(2﹣sin2,1﹣cos2)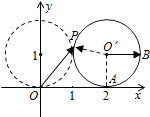
【考點精析】利用圓的參數方程對題目進行判斷即可得到答案,需要熟知圓![]() 的參數方程可表示為
的參數方程可表示為![]() .
.


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數方程為
,其參數方程為![]() (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸,建立極坐標系,曲線
軸的非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lg(1-x)+lg(1+x)+x4-2x2.
(1)求函數f(x)的定義域;
(2)判斷函數f(x)的奇偶性;
(3)求函數f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了解高二學生![]() 、
、![]() 兩個學科學習成績的合格情況是否有關,隨機抽取了該年級一次期末考試
兩個學科學習成績的合格情況是否有關,隨機抽取了該年級一次期末考試![]() 、
、![]() 兩個學科的合格人數與不合格人數,得到以下2
兩個學科的合格人數與不合格人數,得到以下2![]() 2列聯表:
2列聯表:
|
| 合計 | |
| 40 | 20 | 60 |
| 20 | 30 | 50 |
合計 | 60 | 50 | 110 |
(1)據此表格資料,能否在犯錯的概率不超過0.01的前提下認為“![]() 學科合格”與“
學科合格”與“![]() 學科合格”有關;
學科合格”有關;
(2)從“![]() 學科合格”的學生中任意抽取2人,記被抽取的2名學生中“
學科合格”的學生中任意抽取2人,記被抽取的2名學生中“![]() 學科合格”的人數為
學科合格”的人數為![]() ,求
,求![]() 的數學期望.
的數學期望.
附公式與表:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= ![]() ,g(x)=ax2+bx(a,b∈R,a≠0)若y=f(x)的圖象與y=g(x)圖象有且僅有兩個不同的公共點A(x1 , y1),B(x2 , y2),則下列判斷正確的是( )
,g(x)=ax2+bx(a,b∈R,a≠0)若y=f(x)的圖象與y=g(x)圖象有且僅有兩個不同的公共點A(x1 , y1),B(x2 , y2),則下列判斷正確的是( )
A.當a<0時,x1+x2<0,y1+y2>0
B.當a<0時,x1+x2>0,y1+y2<0
C.當a>0時,x1+x2<0,y1+y2<0
D.當a>0時,x1+x2>0,y1+y2>0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正三棱柱(底面為正三角形的直棱柱)ABC-A1B1C1中,已知AB=AA1=2,點Q為BC的中點.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求點![]() 到平面AQC1的距離.
到平面AQC1的距離.
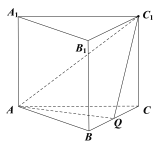
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在2007全運會上兩名射擊運動員甲、乙在比賽中打出如下成績:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用莖葉圖表示甲,乙兩個成績;并根據莖葉圖分析甲、乙兩人成績;
(2)分別計算兩個樣本的平均數![]() 和標準差
和標準差![]() ,并根據計算結果估計哪位運動員的成績比較穩定.
,并根據計算結果估計哪位運動員的成績比較穩定.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】行駛中的汽車,在剎車時由于慣性作用,要繼續往前滑行一段距離才能停下,這段距離叫做剎車距離,在某種路面上,某種型號的汽車的剎車距離s(m)與汽車的車速v(m/s)滿足下列關系:![]() (n為常數,且
(n為常數,且![]() ),做了兩次剎車實驗,發現實驗數據如圖所示其中
),做了兩次剎車實驗,發現實驗數據如圖所示其中

(1)求出n的值;
(2)要使剎車距離不超過12.6米,則行駛的最大速度應為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地鐵換乘站設有編號為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的五個安全出口.若同時開放其中的兩個安全出口,疏散1000名乘客所需的時間如下:
的五個安全出口.若同時開放其中的兩個安全出口,疏散1000名乘客所需的時間如下:
安全出口編號 |
|
|
|
|
|
疏散乘客時間( | 186 | 125 | 160 | 175 | 145 |
則疏散乘客最快的一個安全出口的編號是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com