分析:根據分段函數解析式畫出圖象,如圖所示,先求出f(x)=x2-2x-2與f(x)=1的交點坐標,然后根據交點的橫坐標及函數圖象,即可得到f(x0)>1時,x0的取值范圍.
解答:解:根據題意畫出圖形,如圖所示:
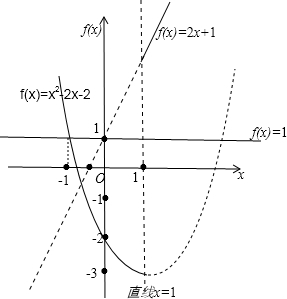
令f(x)=x
2-2x-2=1,即(x-3)(x+1)=0,
解得:x
1=3(舍去),x
2=-1,
根據分段函數的圖象可得:
當f(x
0)>1時,x
0的取值范圍為(-∞,-1)∪[1,+∞).
故答案為:(-∞,-1)∪[1,+∞)
點評:本題主要考查了一元二次不等式的解法,利用了數形結合的數學思想.對于分段函數的有關不等式的解法,可依據圖象法解決.能準確的畫出分段函數的圖象是解本題的關鍵.




 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案