
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1 . 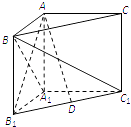
(1)求證:AB1⊥平面A1BC1;
(2)若D為B1C1的中點,求AD與平面A1BC1所成的角.
【答案】
(1)證明:由題意知四邊形AA1B1B是正方形,
∴AB1⊥BA1.
∵AA1⊥平面A1B1C1,∴AA1⊥A1C1.
又∵A1C1⊥A1B1,∴A1C1⊥平面AA1B1B,
∴A1C1⊥AB1.
∴AB1⊥平面A1BC1.
(2)解:設AB1與A1B相交于點O,則點O是線段AB1的中點.
連接AC1,由題意知△AB1C1是正三角形.
由AD,C1O是△AB1C1的中線知:AD與C1O的交點為重心G,連接OG.
由(1) 知AB1⊥平面A1BC1,
∴OG是AD在平面A1BC1上的射影,
∴∠AGO是AD與平面A1BC1所成的角.
在直角△AOG中,
AG= ![]() AD=
AD= ![]() AB1=
AB1= ![]() AB,AO=
AB,AO= ![]() AB,
AB,
∴sin∠AGO= ![]() =
= ![]() .
.
∴∠AGO=60°,
即AD與平面A1BC1所成的角為60°.

【解析】(1)由題意先推導出A1C1⊥平面AA1B1B,從而得到A1C1⊥AB1 , 由此能夠證明AB1⊥平面A1BC1 . (2) 設AB1與A1B相交于點O,由題設條件推導出AD與C1O的交點為重心G,連接OG,能推導出∠AGO是AD與平面A1BC1所成的角,由此能求出AD與平面A1BC1所成的角的大小.
【考點精析】關于本題考查的直線與平面垂直的判定和空間角的異面直線所成的角,需要了解一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想;已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則 才能得出正確答案.
才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】設△ABC的內角A、B、C的對邊分別為a、b、c,a=btanA,且B為鈍角.
(1)證明:B﹣A= ![]() ;
;
(2)求sinA+sinC的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人想參加《中國詩詞大會》比賽,籌辦方要從10首詩司中分別抽出3首讓甲、乙背誦,規定至少背出其中2首才算合格; 在這10首詩詞中,甲只能背出其中的7首,乙只能背出其中的8首
(1)求抽到甲能背誦的詩詞的數量![]() 的分布列及數學期望;
的分布列及數學期望;
(2)求甲、乙兩人中至少且有一人能合格的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設{an}是等差數列,{bn}是各項都為正數的等比數列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an}、{bn}的通項公式;
(2)求數列 ![]() 的前n項和Sn .
的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
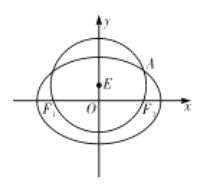
【題目】如圖,已知圓![]() 經過橢圓
經過橢圓![]() 的左右焦點
的左右焦點![]() ,與橢圓
,與橢圓![]() 在第一象限的交點為
在第一象限的交點為![]() ,且
,且![]() ,
, ![]() ,
, ![]() 三點共線.
三點共線.
(1)求橢圓![]() 的方程;
的方程;
(2)設與直線![]() (
(![]() 為原點)平行的直線交橢圓
為原點)平行的直線交橢圓![]() 于
于![]() 兩點,當
兩點,當![]() 的面積取取最大值時,求直線
的面積取取最大值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
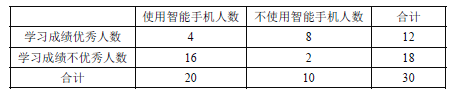
【題目】某研究型學習小組調查研究”中學生使用智能手機對學習的影響”.部分統計數據如下表:
參考數據:

參考公式: 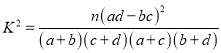 ,其中
,其中![]()
(Ⅰ)試根據以上數據,運用獨立性檢驗思想,指出有多大把握認為中學生使用智能手機對學習有影響?
(Ⅱ)研究小組將該樣本中使用智能手機且成績優秀的4位同學記為![]() 組,不使用智能手機且成績優秀的8位同學記為
組,不使用智能手機且成績優秀的8位同學記為![]() 組,計劃從
組,計劃從![]() 組推選的2人和
組推選的2人和![]() 組推選的3人中,隨機挑選兩人在學校升旗儀式上作“國旗下講話”分享學習經驗.求挑選的兩人恰好分別來自
組推選的3人中,隨機挑選兩人在學校升旗儀式上作“國旗下講話”分享學習經驗.求挑選的兩人恰好分別來自![]() 、
、![]() 兩組的概率.
兩組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() 的直角坐標為
的直角坐標為![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于不同的兩點
相交于不同的兩點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=sin(ωx+ ![]() )(ω>0)的圖象的相鄰兩條對稱軸間的距離是
)(ω>0)的圖象的相鄰兩條對稱軸間的距離是 ![]() .若將函數f(x)的圖象向右平移
.若將函數f(x)的圖象向右平移 ![]() 個單位,再把圖象上每個點的橫坐標縮小為原來的一半,得到g(x),則g(x)的解析式為( )
個單位,再把圖象上每個點的橫坐標縮小為原來的一半,得到g(x),則g(x)的解析式為( )
A.g(x)=sin(4x+ ![]() )
)
B.g(x)=sin(8x﹣ ![]() )??
)??
C.g(x)=sin(x+ ![]() )
)
D.g(x)=sin4x
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com