
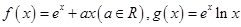 (e為自然對數的底數).
(e為自然對數的底數).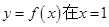 處的切線為
處的切線為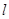 ,若
,若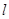 與點(1,0)的距離為
與點(1,0)的距離為 ,求a的值;
,求a的值;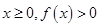 恒成立,試確定
恒成立,試確定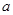 的取值范圍;
的取值范圍; 上是否存在極值?若存在,請求出極值;若不存在,請說明理由.
上是否存在極值?若存在,請求出極值;若不存在,請說明理由.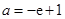 或
或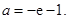 (2)
(2)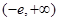 (3)不存在
(3)不存在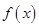 即可得到切點的縱坐標,對
即可得到切點的縱坐標,對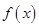 進行求導并得到在切點處的導函數值即為切線的斜率,有切線的斜率,切線又過切點,利用直線的點斜式即可求的切線的方程,利用點到直線的距離公式結合條件點
進行求導并得到在切點處的導函數值即為切線的斜率,有切線的斜率,切線又過切點,利用直線的點斜式即可求的切線的方程,利用點到直線的距離公式結合條件點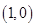 到切線的距離為
到切線的距離為 即可求的參數
即可求的參數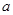 的值.
的值.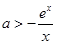 ,則
,則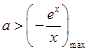 ,再利用函數的導函數研究函數
,再利用函數的導函數研究函數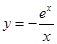 在區間
在區間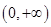 的最大值,即可求的a的取值范圍.
的最大值,即可求的a的取值范圍.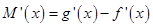 在區間
在區間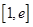 有零點且在零點附近的符號不同,求導可得
有零點且在零點附近的符號不同,求導可得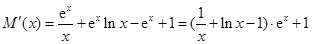 ,設
,設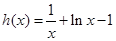 ,求
,求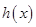 求導可以得到
求導可以得到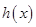 的導函數在區間
的導函數在區間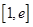 恒為正數,則函數
恒為正數,則函數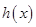 在區間
在區間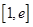 上是單調遞增,即可得到函數
上是單調遞增,即可得到函數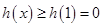 進而得到
進而得到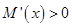 恒成立,即
恒成立,即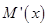 在區間
在區間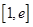 上沒有零點,進而函數
上沒有零點,進而函數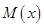 沒有極值.
沒有極值.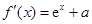 ,
,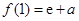 .
.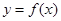 在
在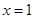 處的切線斜率為
處的切線斜率為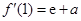 , 1分
, 1分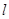 的方程為
的方程為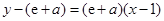 ,即
,即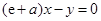 . 3分
. 3分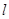 與點
與點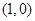 距離為
距離為 ,所以
,所以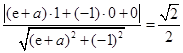 ,
,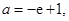 或
或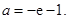 5分
5分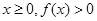 恒成立,
恒成立,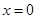 ,則
,則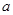 為任意實數時,
為任意實數時,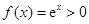 恒成立; 6分
恒成立; 6分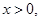
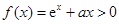 恒成立,即
恒成立,即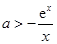 ,在
,在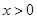 上恒成立, 7分
上恒成立, 7分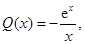 則
則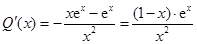 , 8分
, 8分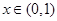 時,
時,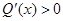 ,則
,則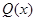 在
在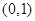 上單調遞增;
上單調遞增;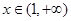 時,
時,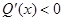 ,則
,則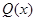 在
在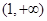 上單調遞減;
上單調遞減;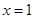 時,
時,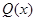 取得最大值,
取得最大值,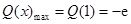 , 9分
, 9分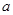 的取值范圍為
的取值范圍為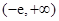 .
.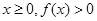 恒成立的實數
恒成立的實數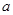 的取值范圍為
的取值范圍為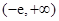 . 10分
. 10分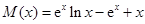 ,
, , 2分
, 2分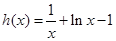 ,則
,則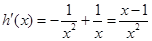 ,當
,當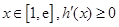 ,
,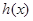 在
在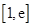 上單調增函數,因此
上單調增函數,因此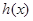 在
在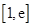 上的最小值為
上的最小值為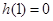 ,
,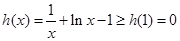 , 12分
, 12分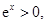 所以在
所以在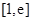 上,
上,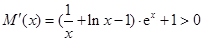 ,
,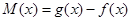 在
在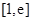 上不存在極值. 14分
上不存在極值. 14分

科目:高中數學 來源:不詳 題型:解答題
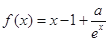 (
(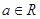 ,
,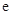 為自然對數的底數).
為自然對數的底數).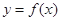 在點
在點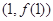 處的切線平行于
處的切線平行于 軸,求
軸,求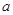 的值;
的值;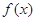 的極值;
的極值;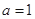 的值時,若直線
的值時,若直線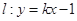 與曲線
與曲線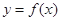 沒有公共點,求
沒有公共點,求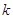 的最大值.
的最大值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.xsinx |
| B.xsinx-xcosx |
| C.xsinx+cosx |
| D.xcosx |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com