
(2005
福建,20)如下圖,直二面角D—AB—E中,四邊形ABCD是邊長為2的正方形,AE=EB,F為CE上的點(diǎn),且BF⊥平面ACE.(1)
求證AE⊥平面BCE;(2)
求二面角B—AC—E的大小;(3)
求點(diǎn)D到平面ACE的距離.
|
解析 (1)∵BF⊥平面ACE,∴BF⊥AE.∵二面角D—AB—E為直二面角,且CB⊥AB,∴CB⊥平面ABE,∴CB⊥AE,∴AE⊥平面BCE.(2) 以線段AB的中點(diǎn)為原點(diǎn)O,OE所在直線為x軸,AB所在直線為y軸,過O點(diǎn)平行于AD的直線為z軸,建立空間直角坐標(biāo)系O-xyz,如下圖.因?yàn)?/FONT>AE⊥面BCE,BE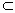 面BCE,所以AE⊥BE,在Rt△AEB中,AB=2,O為AB的中點(diǎn),故OE=1.于是A(0,-l,0),E(1,0,0),C(0,1,2). 面BCE,所以AE⊥BE,在Rt△AEB中,AB=2,O為AB的中點(diǎn),故OE=1.于是A(0,-l,0),E(1,0,0),C(0,1,2).
 .設(shè)平面AEC的一個法向量為n=(x,y,z),則 .設(shè)平面AEC的一個法向量為n=(x,y,z),則 即 即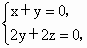
解得  令y=-1,得n=(1,-1,1)是平面AEC的一個法向量.又平面BAC的一個法向量為m=(1,0,0), 令y=-1,得n=(1,-1,1)是平面AEC的一個法向量.又平面BAC的一個法向量為m=(1,0,0),
故 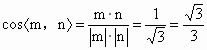 . .
∴二面角 B—AC—E的大小為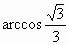 . .
(3) ∵AD∥z軸,AD=2,故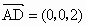 . .
∴點(diǎn) D到平面ACE的距離
|
|
剖析: 1.在平面BCE內(nèi)尋找兩條相交直線都與AE垂直,結(jié)合題設(shè)可知,BF和BC即是.2 .找二面角B—AC—E的平面角.∵ BF⊥平面AEC,只需作BG⊥AC于G,連FG即可;而ABCD為正方形,所以G為AC和BD的交點(diǎn).3 .用體積法較方便. |


 53隨堂測系列答案
53隨堂測系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com