
(12分)拋物線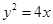 的焦點為
的焦點為 ,過點
,過點 的直線交拋物線于
的直線交拋物線于 ,
,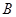 兩點.
兩點.
①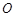 為坐標原點,求證:
為坐標原點,求證: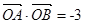 ;
;
②設點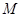 在線段
在線段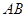 上運動,原點
上運動,原點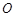 關于點
關于點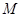 的對稱點為
的對稱點為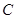 ,求四邊形
,求四邊形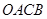 面積的最小值..
面積的最小值..
(Ⅰ)見解析;(Ⅱ) 時,四邊形
時,四邊形 的面積最小,最小值是
的面積最小,最小值是 .
.
【解析】
試題分析:(1)先利用已知條件設出直線AB的方程,與拋物線聯立方程組,然后結合韋達定理表示出向量的數量積,進而證明。
(2)根據由點 與原點
與原點 關于點
關于點 對稱,得
對稱,得 是線段
是線段 的中點,從而點
的中點,從而點 與點
與點 到直線
到直線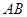 的距離相等,得到四邊形
的距離相等,得到四邊形 的面積等于
的面積等于 ,結合三角形面積公式得到。
,結合三角形面積公式得到。
(Ⅰ)解:依題意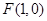 ,設直線
,設直線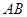 方程為
方程為 . …………1分
. …………1分
將直線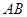 的方程與拋物線的方程聯立,消去
的方程與拋物線的方程聯立,消去 得
得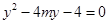 .……3分
.……3分
設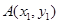 ,
,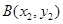 ,所以
,所以
 ,
, .
.
 =1,
=1,
故 .………………6分
.………………6分
(Ⅱ)解:由點 與原點
與原點 關于點
關于點 對稱,得
對稱,得 是線段
是線段 的中點,從而點
的中點,從而點 與點
與點 到直線
到直線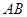 的距離相等,所以四邊形
的距離相等,所以四邊形 的面積等于
的面積等于 .……8分
.……8分
因為  ……………9分
……………9分
 ,…………11分
,…………11分
所以  時,四邊形
時,四邊形 的面積最小,最小值是
的面積最小,最小值是 . ……12分
. ……12分
考點:本試題主要是考查了直線與拋物線愛你的位置關系的運用。
點評:對于幾何中的四邊形的面積一般運用轉換與化歸的思想來求解得到。


 智能訓練練測考系列答案
智能訓練練測考系列答案 計算高手系列答案
計算高手系列答案科目:高中數學 來源:2012-2013學年遼寧省高三第五次模擬理數試卷(解析版) 題型:解答題
(本小題滿分12分)
如圖,已知拋物線 的焦點為
的焦點為 .過點
.過點 的直線交拋物線于
的直線交拋物線于 ,
, 兩點,直線
兩點,直線 ,
, 分別與拋物線交于點
分別與拋物線交于點 ,
, .
.

(Ⅰ)求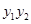 的值;
的值;
(Ⅱ)記直線 的斜率為
的斜率為 ,直線
,直線 的斜率為
的斜率為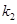 .證明:
.證明: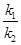 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年海南省瓊海市高考模擬測試理科數學試卷 題型:解答題
已知拋物線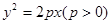 的焦點為
的焦點為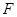 ,過點
,過點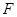 作直線
作直線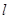 與拋物線交于
與拋物線交于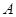 、
、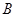 兩點,拋物線的準線與
兩點,拋物線的準線與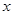 軸交于點
軸交于點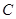 .
.
(1)證明: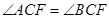 ;
;
2)求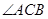 的最大值,并求
的最大值,并求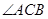 取得最大值時線段
取得最大值時線段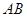 的長.
的長.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省臺州市高三上學期期末文科數學試卷 題型:解答題
已知拋物線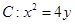 的焦點為
的焦點為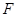 ,過點
,過點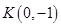 的直線
的直線 與
與 相交于
相交于 兩點,點
兩點,點 關于
關于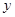 軸的對稱點為
軸的對稱點為 .
.
(Ⅰ)證明:點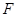 在直線
在直線 上;
上;
(Ⅱ)設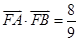 ,求
,求 的平分線與
的平分線與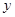 軸的交點坐標.
軸的交點坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com