
| an |
| 1+2an |
| n(n+1) |
| 12 |
| an |
| 1+2an |
| 1 |
| 1+2×1 |
| 1 |
| 3 |
| ||
1+2×
|
| 1 |
| 5 |
| ||
1+2×
|
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| 2×1-1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2k-1 |
| ak |
| 1+2ak |
| ||
1+2×
|
| 1 |
| 2k-1+2 |
| 1 |
| 2k+1 |
| 1 |
| 2(k+1)-1 |
| 1 |
| 2n-1 |
| n(n+1) |
| 12 |
| 1 |
| 6 |
| 1 |
| 2 |
| n(n+1) |
| 12 |
| k(k+1) |
| 12 |
| k(k+1) |
| 12 |
| (k+1)(k+2) |
| 12 |
| (k+1)(k+2) |
| 12 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| an |
| 1+2an |
| n(n+1) |
| 12 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 4x |
| a |
| 2x |
查看答案和解析>>
科目:高中數學 來源:2012屆山東省濰坊市四縣一校高三教學質量監測理科數學 題型:解答題
(本小題滿分12分)(考生注意:本題請從以下甲乙兩題中任選一題作答,若兩題都答 只以甲題計分)
只以甲題計分)
甲:設數列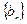 的前
的前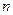 項和為
項和為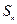 ,且
,且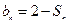 ;數列
;數列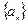 為等差數列,且
為等差數列,且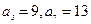
(Ⅰ)求數列 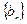 的通項公式
的通項公式
(Ⅱ)若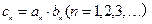 ,
,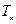 為數列
為數列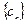 的前
的前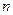
 項和,求
項和,求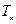
乙:定義在[-1,1]上的奇函數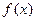 ,已知當
,已知當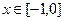 時,
時,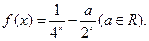
(Ⅰ)求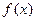 在[0,1]上的最大值
在[0,1]上的最大值
(Ⅱ)若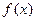 是[0,1]上的增函數,求實數
是[0,1]上的增函數,求實數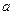 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省濰坊市四縣一校高三教學質量監測理科數學 題型:解答題
(本小題滿分12分)(考生注意:本題請從以下甲乙兩題中任選一題作答,若兩題都答 只以甲題計分)
甲:設數列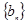 的前
的前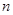 項和為
項和為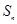 ,且
,且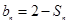 ;數列
;數列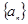 為等差數列,且
為等差數列,且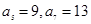
(Ⅰ)求數列 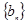 的通項公式
的通項公式
(Ⅱ)若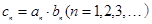 ,
, 為數列
為數列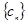 的前
的前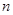 項和,求
項和,求
乙:定義在[-1,1]上的奇函數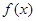 ,已知當
,已知當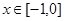 時,
時,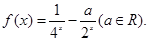
(Ⅰ)求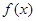 在[0,1]上的最大值
在[0,1]上的最大值
(Ⅱ)若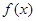 是[0,1]上的增函數,求實數
是[0,1]上的增函數,求實數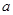 的取值范圍
的取值范圍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com