
【題目】已知函數![]() .
.
(1)若曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)討論方程![]() 的實數根的情況.
的實數根的情況.
【答案】(1)![]() (2)當
(2)當![]() 時,方程有兩個實數根;當
時,方程有兩個實數根;當![]() 時,方程無實數根.
時,方程無實數根.
【解析】試題分析: (1)求出![]() ,利用兩直線垂直,求出
,利用兩直線垂直,求出![]() 的值; (2)設
的值; (2)設![]() ,利用單調性求出
,利用單調性求出![]() , 分類討論:
, 分類討論: ![]() ,得出結果.
,得出結果.
試題解析:(1)依題意,得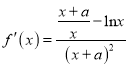 ,
,
所以![]() ,
,
又由曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直,可得
垂直,可得![]() ,
,
所以![]() ,解得
,解得![]() ;
;
(2)方程![]() ,即
,即![]() .
.
當![]() 時,得
時,得![]() ,解得
,解得![]() ,
,
當![]() 時,解得
時,解得![]() .但是
.但是![]() ,即
,即![]() ,所以
,所以![]() 時,方程無實數根.
時,方程無實數根.
令![]() ,則
,則![]() ,
,
故當![]() 時,
時, ![]() 是單調遞增函數;當
是單調遞增函數;當![]() 時,
時, ![]() 是單調遞減函數,
是單調遞減函數,
所以![]() .
.
當![]() 時,由
時,由![]() ,得
,得![]() .
.
又![]() ,令
,令![]() ,則
,則![]() 在區間
在區間![]() 上
上![]() ,故
,故![]() 為增函數,所以
為增函數,所以![]() ,即
,即![]() ,所以
,所以![]() .
.
![]() ,故當
,故當![]() 時,方程有兩個實數根;當
時,方程有兩個實數根;當![]() 時,方程無實數根.
時,方程無實數根.
點睛: 本題主要考查了導數的幾何意義以及函數零點的個數,屬于中檔題.
【一題多解】在(2)中,由![]() 有
有![]() ,轉化為函數
,轉化為函數![]() 與
與![]() 圖象交點的個數,當
圖象交點的個數,當![]() 與
與![]() 相切時,切點為
相切時,切點為![]() ,又
,又![]() ,所以此時無零點;由圖象知,當
,所以此時無零點;由圖象知,當![]() 時圖象有兩個交點,即有兩個零點,
時圖象有兩個交點,即有兩個零點, ![]() ,圖象沒有交點,無零點,綜上討論,得出結論:
,圖象沒有交點,無零點,綜上討論,得出結論: ![]() 有兩個實數根,
有兩個實數根, ![]() 無實數根.
無實數根.


 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
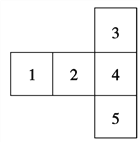
【題目】編號為A,B,C,D,E的5個小球放在如圖所示的5個盒子里,要求每個盒子只能放1個小球,且A球不能放在1,2號盒子里,B球必須放在與A球相鄰的盒子中,求不同的放法有多少種?
查看答案和解析>>
科目:高中數學 來源: 題型:
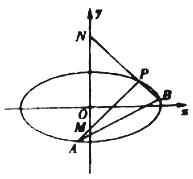
【題目】已知直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,與
兩點,與![]() 軸,
軸, ![]() 軸分別相交于點
軸分別相交于點![]() 和點
和點![]() ,且
,且![]() ,點
,點![]() 是點
是點![]() 關于
關于![]() 軸的對稱點,
軸的對稱點, ![]() 的延長線交橢圓于點
的延長線交橢圓于點![]() ,過點
,過點![]() 分別做
分別做![]() 軸的垂線,垂足分別為
軸的垂線,垂足分別為![]() .
.
(1) 若橢圓![]() 的左、右焦點與其短軸的一個端點是正三角形的三個頂點,點
的左、右焦點與其短軸的一個端點是正三角形的三個頂點,點![]() 在橢圓
在橢圓![]() 上,求橢圓
上,求橢圓![]() 的方程;
的方程;
(2)當![]() 時,若點
時,若點![]() 平分線段
平分線段![]() ,求橢圓
,求橢圓![]() 的離心率.
的離心率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某土特產銷售總公司為了解其經營狀況,調查了其下屬各分公司月銷售額和利潤,得到數據如下表:
分公司名稱 | 雅雨 | 雅魚 | 雅女 | 雅竹 | 雅茶 |
月銷售額 | 3 | 5 | 6 | 7 | 9 |
月利潤額 | 2 | 3 | 3 | 4 | 5 |
在統計中發現月銷售額![]() 和月利潤額
和月利潤額![]() 具有線性相關關系.
具有線性相關關系.
(1)根據如下的參考公式與參考數據,求月利潤額![]() 與月銷售額
與月銷售額![]() 之間的線性回歸方程;
之間的線性回歸方程;
(2)若該總公司還有一個分公司“雅果”月銷售額為10萬元,試估計它的月利潤額是多少?
(參考公式: 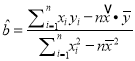 ,
, ![]() ,其中:
,其中: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的離心率為
)的離心率為![]() ,以橢圓的四個頂點為頂點的四邊形的面積為8.
,以橢圓的四個頂點為頂點的四邊形的面積為8.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)如圖,斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,點
兩點,點![]() 在直線
在直線![]() 的左上方.若
的左上方.若![]() ,且直線
,且直線![]() ,
, ![]() 分別與
分別與![]() 軸交于
軸交于![]() ,
, ![]() 點,求線段
點,求線段![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
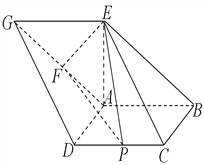
【題目】如圖,已知四邊形![]() 和
和![]() 均為平行四邊形,點
均為平行四邊形,點![]() 在平面
在平面![]() 內的射影恰好為點
內的射影恰好為點![]() ,以
,以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ,
, ![]() ,
, ![]() 的中點為
的中點為![]() ,
, ![]() 的中點為
的中點為![]() ,且
,且![]() .
.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求幾何體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地最近十年糧食需求量逐年上升,下表是部分統計數據:
年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
需求量(萬噸) | 236 | 246 | 257 | 276 | 286 |
(1)利用所給數據求年需求量與年份之間的回歸方程![]() =
=![]() x+
x+![]() ;
;
(2)利用(1)中所求出的直線方程預測該地2018年的糧食需求量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)用定義證明函數![]() 在
在![]() 上是增函數;
上是增函數;
(2)探究是否存在實數![]() ,使得函數
,使得函數![]() 為奇函數?若存在,求出
為奇函數?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(3)在(2)的條件下,解不等式![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com