
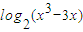 ]的圖象為曲線C1求與直線4x+15y-3=0垂直的曲線C1的切線方程;
]的圖象為曲線C1求與直線4x+15y-3=0垂直的曲線C1的切線方程;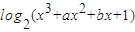 ]的圖象為曲線C2,若存在實數(shù)b使得曲線C2在x(x∈(1,4))處有斜率為-8的切線,求實數(shù)a的取值范圍;
]的圖象為曲線C2,若存在實數(shù)b使得曲線C2在x(x∈(1,4))處有斜率為-8的切線,求實數(shù)a的取值范圍;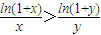 ,構造函數(shù)h(x)=
,構造函數(shù)h(x)= ,利用導數(shù)判斷h(x)單調(diào)遞減即可.
,利用導數(shù)判斷h(x)單調(diào)遞減即可.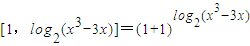 =x3-3x,
=x3-3x,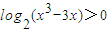 ,得x3-3x>1.又
,得x3-3x>1.又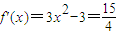 ,由f′(x)=0,得x=
,由f′(x)=0,得x=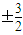 ,
,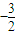 .又f(-
.又f(- )=
)= ,∴切點為(
,∴切點為(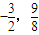 ).
).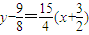 ,即15x-4y+27=0.
,即15x-4y+27=0.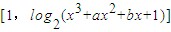 =x3+ax2+bx+1.
=x3+ax2+bx+1.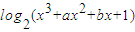 >0,得x3+ax2+bx>0,
>0,得x3+ax2+bx>0,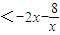 在(1,4)上有解,∴a
在(1,4)上有解,∴a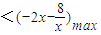 (1<x<4),
(1<x<4),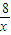 =-(2x+
=-(2x+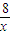 )≤-2
)≤-2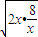 =-8,當且僅當x=2時取等號,∴a<-8.
=-8,當且僅當x=2時取等號,∴a<-8.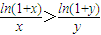 ,
,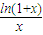 ,則
,則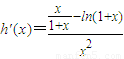 ,當x≥2時,
,當x≥2時,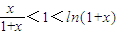 ,
,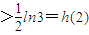 .
.

科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
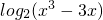 ]的圖象為曲線C1求與直線4x+15y-3=0垂直的曲線C1的切線方程;
]的圖象為曲線C1求與直線4x+15y-3=0垂直的曲線C1的切線方程;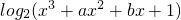 ]的圖象為曲線C2,若存在實數(shù)b使得曲線C2在x0(x0∈(1,4))處有斜率為-8的切線,求實數(shù)a的取值范圍;
]的圖象為曲線C2,若存在實數(shù)b使得曲線C2在x0(x0∈(1,4))處有斜率為-8的切線,求實數(shù)a的取值范圍;查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源:《導數(shù)及其應用》2013年高三數(shù)學一輪復習單元訓練(北京郵電大學附中)(解析版) 題型:解答題
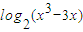 ]的圖象為曲線C1求與直線4x+15y-3=0垂直的曲線C1的切線方程;
]的圖象為曲線C1求與直線4x+15y-3=0垂直的曲線C1的切線方程; ]的圖象為曲線C2,若存在實數(shù)b使得曲線C2在x(x∈(1,4))處有斜率為-8的切線,求實數(shù)a的取值范圍;
]的圖象為曲線C2,若存在實數(shù)b使得曲線C2在x(x∈(1,4))處有斜率為-8的切線,求實數(shù)a的取值范圍;查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com