
【題目】設集合![]() 是集合
是集合![]() …,
…,![]() 的子集.記
的子集.記![]() 中所有元素的和為
中所有元素的和為![]() (規定:
(規定:![]() 為空集時,
為空集時,![]() =0).若
=0).若![]() 為3的整數倍,則稱
為3的整數倍,則稱![]() 為
為![]() 的“和諧子集”.
的“和諧子集”.
求:(1)集合![]() 的“和諧子集”的個數;
的“和諧子集”的個數;
(2)集合![]() 的“和諧子集”的個數.
的“和諧子集”的個數.
【答案】(1)![]() 的“和諧子集”的個數等于4.(2)
的“和諧子集”的個數等于4.(2)![]()
【解析】
(1)由集合的子集可得:集合A1的“和諧子集”為::,{3},![]() 共4個,
共4個,
(2)由即時定義的理解,分類討論的數學思想方法可得:討論集合An+1={1,2,3,……,3n﹣2,3n﹣1,3n,3n+1,3n+2,3n+3}中的“和諧子集”的情況,以新增元素3n+1,3n+2,3n+3為標準展開討論即可得解
(1)集合![]() 的子集有:
的子集有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中所有元素和為3的整數倍的集合有:![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() 的“和諧子集”的個數等于4.
的“和諧子集”的個數等于4.
(2)記![]() 的“和諧子集”的個數等于
的“和諧子集”的個數等于![]() ,即
,即![]() 有
有![]() 個所有元素和為3的整數倍的子集;
個所有元素和為3的整數倍的子集;
另記![]() 有
有![]() 個所有元素和為3的整數倍余1的子集,有
個所有元素和為3的整數倍余1的子集,有![]() 個所有元素和為3的整數
個所有元素和為3的整數
倍余2的子集.
由(1)知,![]() .
.
集合 的“和諧子集”
的“和諧子集”
有以下四類(考查新增元素![]() ):
):
第一類 集合![]() …,
…,![]() 的“和諧子集”,共
的“和諧子集”,共![]() 個;
個;
第二類 僅含一個元素![]() 的“和諧子集”,共
的“和諧子集”,共![]() 個;
個;
同時含兩個元素![]() 的“和諧子集”,共
的“和諧子集”,共![]() 個;
個;
同時含三個元素![]() 的“和諧子集”,共
的“和諧子集”,共![]() 個;
個;
第三類 僅含一個元素![]() 的“和諧子集”,共
的“和諧子集”,共![]() 個;
個;
同時含兩個元素![]() 的“和諧子集”,共
的“和諧子集”,共![]() 個;
個;
第四類 僅含一個元素![]() 的“和諧子集”,共
的“和諧子集”,共![]() 個;
個;
同時含有兩個元素![]() 的“和諧子集”,共
的“和諧子集”,共![]() 個,
個,
所以集合![]() 的“和諧子集”共有
的“和諧子集”共有![]() 個.
個.
同理得![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,
所以數列![]() 是以2為首項,公比為2 的等比數列.
是以2為首項,公比為2 的等比數列.
所以![]() .同理得
.同理得![]() .
.
又![]() ,所以
,所以![]() .
.


科目:高中數學 來源: 題型:
【題目】為考察某動物疫苗預防某種疾病的效果,現對200只動物進行調研,并得到如下數據:
未發病 | 發病 | 合計 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合計 | 100 | 100 | 200 |
(附: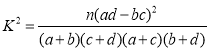 )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
則下列說法正確的:( )
A.至少有99.9%的把握認為“發病與沒接種疫苗有關”
B.至多有99%的把握認為“發病與沒接種疫苗有關”
C.至多有99.9%的把握認為“發病與沒接種疫苗有關”
D.“發病與沒接種疫苗有關”的錯誤率至少有0.01%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據一組樣本數據(xi,yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為![]() =0.85x-85.71,則下列結論中不正確的是
=0.85x-85.71,則下列結論中不正確的是
A. y與x具有正的線性相關關系
B. 回歸直線過樣本點的中心(![]() ,
,![]() )
)
C. 若該大學某女生身高增加1cm,則其體重約增加0.85kg
D. 若該大學某女生身高為170cm,則可斷定其體重比為58.79kg
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新高考方案的實施,學生對物理學科的選擇成了焦點話題. 某學校為了了解該校學生的物理成績,從![]() ,兩個班分別隨機調查了40名學生,根據學生的某次物理成績,得到
,兩個班分別隨機調查了40名學生,根據學生的某次物理成績,得到![]() 班學生物理成績的頻率分布直方圖和
班學生物理成績的頻率分布直方圖和![]() 班學生物理成績的頻數分布條形圖.
班學生物理成績的頻數分布條形圖.

(Ⅰ)估計![]() 班學生物理成績的眾數、中位數(精確到
班學生物理成績的眾數、中位數(精確到![]() )、平均數(各組區間內的數據以該組區間的中點值為代表);
)、平均數(各組區間內的數據以該組區間的中點值為代表);
(Ⅱ)填寫列聯表,并判斷是否有![]() 的把握認為物理成績與班級有關?
的把握認為物理成績與班級有關?
物理成績 | 物理成績 | 合計 | |
| |||
| |||
合計 |
附:![]() 列聯表隨機變量
列聯表隨機變量![]() ;
;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 中心在原點
中心在原點![]() ,焦點在坐標軸上,直線
,焦點在坐標軸上,直線![]() 與橢圓
與橢圓![]() 在第一象限內的交點是
在第一象限內的交點是![]() ,點
,點![]() 在
在![]() 軸上的射影恰好是橢圓
軸上的射影恰好是橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 另一個焦點是
另一個焦點是![]() ,且
,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的直線
的直線![]() 與
與![]() 交于點
交于點![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線與
的直線與![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .若
.若![]() ,且
,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com