
【題目】已知點![]() 在拋物線
在拋物線![]() 上,點
上,點![]() 是拋物線
是拋物線![]() 的焦點,線段
的焦點,線段![]() 的中點為
的中點為![]() .
.
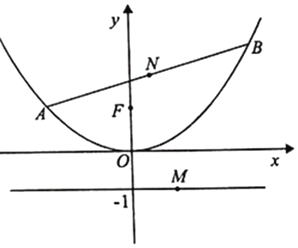
(1)若點![]() 的坐標為
的坐標為![]() ,且
,且![]() 是
是![]() 的垂心,求直線
的垂心,求直線![]() 的方程;
的方程;
(2)若點![]() 是直線
是直線![]() 上的動點,且
上的動點,且![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)2.
;(2)2.
【解析】
(1)求得拋物線的焦點和準線方程,求得![]() 的斜率,可得
的斜率,可得![]() 的斜率,設
的斜率,設![]() 的方程,聯立拋物線方程,運用判別式大于0和韋達定理,運用兩直線垂直的條件,可得
的方程,聯立拋物線方程,運用判別式大于0和韋達定理,運用兩直線垂直的條件,可得![]() 的方程,求得
的方程,求得![]() 的值,即可得到所求直線方程;
的值,即可得到所求直線方程;
(2)顯然![]() 最小,必須
最小,必須![]() 垂直于直線
垂直于直線![]() ,分別過
,分別過![]() ,
,![]() 作
作![]() ,
,![]() 垂直直線
垂直直線![]() ,垂足為
,垂足為![]() ,
,![]() ,運用梯形的中位線定理,以及三點共線取得最小值,即可得到所求最小值.
,運用梯形的中位線定理,以及三點共線取得最小值,即可得到所求最小值.
(1)![]() 的焦點
的焦點![]() ,準線方程為
,準線方程為![]() ,
,
![]() ,
,![]() 為
為![]() 的垂心,可得
的垂心,可得![]() ,即有
,即有![]() ,
,
設![]() 的方程為
的方程為![]() ,代入拋物線方程可得:
,代入拋物線方程可得:
![]() ,可得
,可得![]() ,
,
由![]() ,可得
,可得 ,
,
![]() ,
,
化簡可得![]() ,
,
即為![]() ,解得
,解得![]() ,
,
由![]() ,可得
,可得![]() ,
,
則![]() 的方程為
的方程為![]() ;
;
(2)顯然![]() 最小,必須
最小,必須![]() 垂直于直線
垂直于直線![]() ,
,
分別過![]() 作
作![]() 垂直直線
垂直直線![]() ,垂足為
,垂足為![]() ,
,
![]() ,
,
等號成立當且僅當![]() 三點共線,且
三點共線,且![]() 軸,
軸,
所以![]() 的最小值為2.
的最小值為2.



科目:高中數學 來源: 題型:
【題目】中央電視臺為了解一檔詩歌類節目的收視情況,抽查東西兩部各5個城市,得到觀看該節目的人數(單位:千人)如下莖葉圖所示:
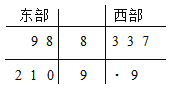
其中一個數字被污損;
(1)求東部各城市觀看該節目觀眾平均人數超過西部各城市觀看該節目觀眾平均人數的概率;
(2)隨著節目的播出,極大激發了觀眾對詩歌知識的學習積累熱情,從中獲益匪淺.現從觀看該節目的觀眾中隨機統計了4位觀眾的周均學習詩歌知識的時間(單位:小時)與年齡(單位:歲),并制作了對照表(如下表所示):

由表中數據,試求線性回歸方程![]() ,并預測年齡在60歲的觀眾周均學習詩歌知識的時間.
,并預測年齡在60歲的觀眾周均學習詩歌知識的時間.
參考公式: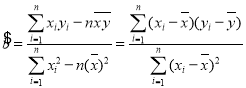 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一個口袋有m個白球,n個黑球(m,n![]()
![]() ,n
,n![]() 2),這些球除顏色外全部相同。現將口袋中的球隨機的逐個取出,并放入如圖所示的編號為1,2,3,……,m+n的抽屜內,其中第k次取球放入編號為k的抽屜(k=1,2,3,……,m+n).
2),這些球除顏色外全部相同。現將口袋中的球隨機的逐個取出,并放入如圖所示的編號為1,2,3,……,m+n的抽屜內,其中第k次取球放入編號為k的抽屜(k=1,2,3,……,m+n).
![]()
(1)試求編號為2的抽屜內放的是黑球的概率p;
(2)隨機變量x表示最后一個取出的黑球所在抽屜編號的倒數,E(x)是x的數學期望,證明 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司有![]() 四輛汽車,其中
四輛汽車,其中![]() 車的車牌尾號為0,
車的車牌尾號為0,![]() 兩輛車的車牌尾號為6,
兩輛車的車牌尾號為6,![]() 車的車牌尾號為5,已知在非限行日,每輛車都有可能出車或不出車.已知
車的車牌尾號為5,已知在非限行日,每輛車都有可能出車或不出車.已知![]() 兩輛汽車每天出車的概率為
兩輛汽車每天出車的概率為![]() ,
,![]() 兩輛汽車每天出車的概率為
兩輛汽車每天出車的概率為![]() ,且四輛汽車是否出車是相互獨立的.
,且四輛汽車是否出車是相互獨立的.
該公司所在地區汽車限行規定如下:

(1)求該公司在星期四至少有2輛汽車出車的概率;
(2)設![]() 表示該公司在星期一和星期二兩天出車的車輛數之和,求
表示該公司在星期一和星期二兩天出車的車輛數之和,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義域是![]() 上的連續函數
上的連續函數![]() 圖像的兩個端點為
圖像的兩個端點為![]() 、
、![]() ,
,![]() 是圖像
是圖像![]() 上任意一點,過點
上任意一點,過點![]() 作垂直于
作垂直于![]() 軸的直線
軸的直線![]() 交線段
交線段![]() 于點
于點![]() (點
(點![]() 與點
與點![]() 可以重合),我們稱
可以重合),我們稱![]() 的最大值為該函數的“曲徑”,下列定義域是
的最大值為該函數的“曲徑”,下列定義域是![]() 上的函數中,曲徑最小的是( )
上的函數中,曲徑最小的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在△ABC中,角A,B,C所對的邊分別為a,b,c,其中A為銳角,且asin(B+C)是![]() bcosC與
bcosC與![]() ccosB的等差中項.
ccosB的等差中項.
(1)求角A的大小;
(2)若點D在△ABC的內部,且滿足∠CAD=∠ABD![]() ,∠CBD
,∠CBD![]() ,AD=1,求CD的長.
,AD=1,求CD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com