
��֪���タ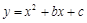 ���c(di��n)
���c(di��n)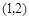 ̎���о��cֱ��
̎���о��cֱ��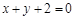 ��ֱ����(sh��)
��ֱ����(sh��)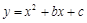 ����ֵ��
����ֵ��
����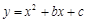 ������
������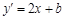 �����Ԓ��タ���c(di��n)
�����Ԓ��タ���c(di��n)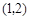 ��̎���о���б�ʞ�
��̎���о���б�ʞ�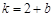 ����?y��n)��о��cֱ��
����?y��n)��о��cֱ��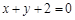 ��ֱ������
��ֱ������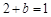 ����
����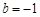 ������?y��n)��c(di��n)
������?y��n)��c(di��n)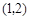 �ڒ��タ�ϣ�����
�ڒ��タ�ϣ�����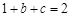 ����
����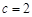 ����?y��n)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052523320510141577/SYS201205252333278353460106_DA.files/image010.png">�����Ǻ���(sh��)�](m��i)����ֵ����(d��ng)
����?y��n)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052523320510141577/SYS201205252333278353460106_DA.files/image010.png">�����Ǻ���(sh��)�](m��i)����ֵ����(d��ng)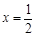 �r(sh��)������Сֵ
�r(sh��)������Сֵ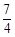 ��
��
������������(j��)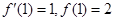 ����b,c�ķ������b,c��Ȼ���ٸ���(j��)���κ���(sh��)�����|(zh��)����ֵ����
����b,c�ķ������b,c��Ȼ���ٸ���(j��)���κ���(sh��)�����|(zh��)����ֵ����



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2012����ͨ�ߵȌW(xu��)У����ȫ��(gu��)�y(t��ng)һ��ԇȫ��(gu��)�픵(sh��)�W(xu��)�Ŀ� �}�ͣ�044
��֪���タC��y��(x��1)2�c�AM��(x��1)2��(y��![]() )2��r2(r��0)��һ��(g��)�����c(di��n)A������A̎���������о���ͬһֱ���ϣ�
)2��r2(r��0)��һ��(g��)�����c(di��n)A������A̎���������о���ͬһֱ���ϣ�
(��)��r��
(��)�O(sh��)m��n�Ǯ���l���cC��M���еăɗlֱ����m��n�Ľ��c(di��n)��D����D��l�ľ��x��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ���߿����} �}�ͣ�����}
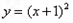 �c�A
�c�A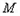 ��
��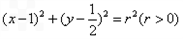 ��һ��(g��)�����c(di��n)
��һ��(g��)�����c(di��n)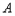 ������
������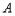 ̎���������о���ͬһֱ���ϡ�
̎���������о���ͬһֱ���ϡ�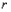 ��
��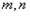 �Ǯ���
�Ǯ��� ���c
���c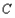 ��
��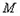 ���еăɗlֱ����
���еăɗlֱ����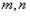 �Ľ��c(di��n)��
�Ľ��c(di��n)��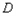 ����
���� ��
�� �ľ��x��
�ľ��x���鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com