
【題目】已知定義在![]() 上的函數
上的函數![]() 和數列
和數列![]() 滿足下列條件:
滿足下列條件:![]() ,
,![]() ,當
,當![]() 且
且![]() 時,
時,![]() 且
且![]() ,其中
,其中![]() 、
、![]() 均為非零常數.
均為非零常數.
(1)若![]() 是等差數列,求實數
是等差數列,求實數![]() 的值;
的值;
(2)令![]() (
(![]() ),若
),若![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(3)令![]() (
(![]() ),若
),若![]() ,數列
,數列![]() 滿足
滿足![]() ,若數列
,若數列![]() 有最大值
有最大值![]() ,最小值
,最小值![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)某公司生產的商品A每件售價為5元時,年銷售10萬件,
(1)據市場調查,若價格每提高一元,銷量相應減少1萬件,要使銷售收入不低于原銷售收入,該商品的銷售價格最多提高多少元?
(2)為了擴大該商品的影響力,公司決定對該商品的生產進行技術革新,將技術革新后生產的商品售價提高到每件![]() 元,公司擬投入
元,公司擬投入![]() 萬元作為技改費用,投入
萬元作為技改費用,投入![]() 萬元作為宣傳費用。試問:技術革新后生產的該商品銷售量m至少應達到多少萬件時,才可能使技術革新后的該商品銷售收入等于原銷售收入與總投入之和?
萬元作為宣傳費用。試問:技術革新后生產的該商品銷售量m至少應達到多少萬件時,才可能使技術革新后的該商品銷售收入等于原銷售收入與總投入之和?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著智能手機和電子閱讀器越來越普及,人們的閱讀習慣也發生了改變,手機和電子閱讀產品方便易攜帶,越來越多的人習慣通過手機或電子閱讀器閱讀.某電子書閱讀器廠商隨機調查了![]() 人,統計了這
人,統計了這![]() 人每日平均通過手機或電子閱讀器閱讀的時間(單位:分鐘),由統計數據得到如下頻率分布直方圖,已知閱讀時間在
人每日平均通過手機或電子閱讀器閱讀的時間(單位:分鐘),由統計數據得到如下頻率分布直方圖,已知閱讀時間在![]() ,
, ![]() ,
, ![]() 三組對應的人數依次成等差數列.
三組對應的人數依次成等差數列.
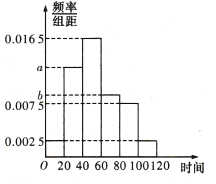
(1)求頻率分布直方圖中![]() ,
, ![]() 的值;
的值;
(2)若將日平均閱讀時間不少于![]() 分鐘的用戶定義為“電子閱讀發燒友”,將日平均閱讀時間少于
分鐘的用戶定義為“電子閱讀發燒友”,將日平均閱讀時間少于![]() 分鐘的用戶定義為“電子閱讀潛在愛好者”,現從上述“電子閱讀發燒友”與“電子閱讀潛在愛好者”的人中按分層抽樣選出
分鐘的用戶定義為“電子閱讀潛在愛好者”,現從上述“電子閱讀發燒友”與“電子閱讀潛在愛好者”的人中按分層抽樣選出![]() 人,再從這
人,再從這![]() 人中任取
人中任取![]() 人,求恰有
人,求恰有![]() 人為“電子閱讀發燒友”的概率.
人為“電子閱讀發燒友”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的中心在原點,焦點在x軸上,離心率等于![]() ,它的一個頂點恰好是拋物線
,它的一個頂點恰好是拋物線![]() 的焦點.
的焦點.
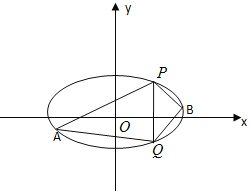
(Ⅰ)求橢圓C的方程;
(Ⅱ)點P(2,3), Q(2,-3)在橢圓上,A,B是橢圓上位于直線PQ兩惻的動點,
①若直線AB的斜率為![]() ,求四邊形APBQ面積的最大值;
,求四邊形APBQ面積的最大值;
②當A、B運動時,滿足于∠APQ=∠BPQ,試問直線AB的斜率是否為定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,
中, ![]() 是坐標原點,設函數
是坐標原點,設函數![]() 的圖象為直線
的圖象為直線![]() ,且
,且![]() 與
與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,給出下列四個命題:
兩點,給出下列四個命題:
①存在正實數![]() ,使
,使![]() 的面積為
的面積為![]() 的直線
的直線![]() 僅有一條;
僅有一條;
②存在正實數![]() ,使
,使![]() 的面積為
的面積為![]() 的直線
的直線![]() 僅有二條;
僅有二條;
③存在正實數![]() ,使
,使![]() 的面積為
的面積為![]() 的直線
的直線![]() 僅有三條;
僅有三條;
④存在正實數![]() ,使
,使![]() 的面積為
的面積為![]() 的直線
的直線![]() 僅有四條.
僅有四條.
其中,所有真命題的序號是( ).
A. ①②③ B. ③④ C. ②④ D. ②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象過原點,且在
的圖象過原點,且在![]() 處取得極值,直線
處取得極值,直線![]() 與曲線
與曲線![]() 在原點處的切線互相垂直.
在原點處的切線互相垂直.
(Ⅰ)求函數![]() 的解析式;
的解析式;
(Ⅱ)若對任意實數的![]() ,恒有
,恒有![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com