
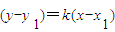 ,代入x2=4y,消元,利用△=0,即可確定
,代入x2=4y,消元,利用△=0,即可確定 ,利用切線過點M(x,y),所以可得
,利用切線過點M(x,y),所以可得 ,同理可得
,同理可得 ,由此可得直線AB的方程,從而可得結論;
,由此可得直線AB的方程,從而可得結論; (k≠0),代入x2=4y,消去y,利用韋達定理
(k≠0),代入x2=4y,消去y,利用韋達定理 的兩實根,故有
的兩實根,故有 ,從而可得
,從而可得 =4m2+m
=4m2+m -4m-
-4m- =(m-1)(
=(m-1)(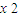 +4m),分類討論,利用
+4m),分類討論,利用 =0,kABkMA=-1,即可求得結論.
=0,kABkMA=-1,即可求得結論. ,代入x2=4y,整理得x2-4kx+4(kx1-y1)=0△=(4k)2-4×4(kx1-y1)=0,又因為
,代入x2=4y,整理得x2-4kx+4(kx1-y1)=0△=(4k)2-4×4(kx1-y1)=0,又因為 ,所以
,所以 …(6分)
…(6分) 即
即
 ①即
①即 …(8分)
…(8分)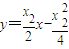 ,
, ②…(10分)
②…(10分) …(6分)
…(6分) 即xx=2(y+y),故直線AB的方程為xx=2(y+y)…(12分)
即xx=2(y+y),故直線AB的方程為xx=2(y+y)…(12分) (k≠0),
(k≠0), ,
, 此時
此時 ,
,
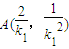 ,
, …(8分)
…(8分) ,
, ,
, ,
, …(11分)
…(11分) ,即xx=2(y+y)…(12分)
,即xx=2(y+y)…(12分)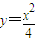 ,求導得
,求導得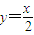 ,切點分別為A(x1,y1),B(x2,y2),故過點A(x1,y1)的切線斜率為
,切點分別為A(x1,y1),B(x2,y2),故過點A(x1,y1)的切線斜率為 ,從而切線方程為
,從而切線方程為 即
即
 ①即
①即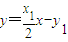 …(8分)
…(8分)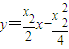 ,
, ②即
②即 …(10分)
…(10分) 即xx=2(y+y),故直線AB的方程為xx=2(y+y)…(12分)
即xx=2(y+y),故直線AB的方程為xx=2(y+y)…(12分) 的兩實根,故有
的兩實根,故有
 ,
, ,y=m
,y=m =4m2+m
=4m2+m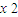 -4m-
-4m- =(m-1)(
=(m-1)( +4m),…(9分)
+4m),…(9分) =0,直線l上任意一點M均有MA⊥MB,△MAB為直角三角形;…(10分)
=0,直線l上任意一點M均有MA⊥MB,△MAB為直角三角形;…(10分) <0,∠AMB>
<0,∠AMB> ,△MAB不可能為直角三角形;…(11分)
,△MAB不可能為直角三角形;…(11分) >0,∠AMB<
>0,∠AMB< ,.
,. =
= =
= ,
, =
= ,
,
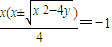 ,整理得(y+2)
,整理得(y+2) =-4,
=-4,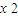 =4,
=4, =4有解的充要條件是m>2,所以當m>2時,有MA⊥AB或MB⊥AB,△MAB為直角三角形…(13分)
=4有解的充要條件是m>2,所以當m>2時,有MA⊥AB或MB⊥AB,△MAB為直角三角形…(13分)

科目:高中數(shù)學 來源: 題型:
 如圖,設拋物線C的方程為y2=4x,O為坐標原點,P為拋物線的準線與其對稱軸的交點,過焦點F且垂直于x軸的直線交拋物線于M、N兩點,若直線PM與ON相交于點Q,則cos∠MQN=
如圖,設拋物線C的方程為y2=4x,O為坐標原點,P為拋物線的準線與其對稱軸的交點,過焦點F且垂直于x軸的直線交拋物線于M、N兩點,若直線PM與ON相交于點Q,則cos∠MQN=
| ||
| 10 |
| ||
| 10 |
查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年廣西桂林市、崇左市、防城港市高考第一次聯(lián)合模擬理科數(shù)學試卷(解析版) 題型:選擇題
設拋物線C的方程為y =4x,O為坐標原點,P為拋物線的準線與其對稱軸的交點,過焦點F且垂直于x軸的直線交拋物線于M、N兩點,若直線PM與ON相交于點Q,則cos∠MQN=
=4x,O為坐標原點,P為拋物線的準線與其對稱軸的交點,過焦點F且垂直于x軸的直線交拋物線于M、N兩點,若直線PM與ON相交于點Q,則cos∠MQN=
A. B.-
B.- C.
C.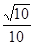 D.-
D.-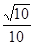
查看答案和解析>>
科目:高中數(shù)學 來源:2011-2012學年廣東省韶關市高三調(diào)研數(shù)學試卷(文科)(解析版) 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源:2012年安徽省合肥六中高三第二次調(diào)研數(shù)學試卷(文科)(解析版) 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源:2011年福建省龍巖市一級達標學校聯(lián)盟高中高三聯(lián)考數(shù)學試卷(理科)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com