
(1)若橢圓C上的點A(1,3[]2)到F1、F2兩點的距離之和等于4,寫出橢圓C的方程和焦點坐標;
(2)設點K是(1)中所得橢圓上的動點,求線段F1K的中點的軌跡方程;
(3)已知橢圓具有性質:若M、N是橢圓C上關于原點對稱的兩個點,點P是橢圓上任意一點,當直線PM、PN的斜率都存在,并記為kPM?,kPN時,那么kPM與kPN之積是與點P位置無關的定值,試寫出雙曲線![]() =1具有類似特性的性質并加以證明.
=1具有類似特性的性質并加以證明.
解:(1)橢圓C的焦點在x軸上,由橢圓上的點A到F1、F2兩點的距離之和是4,得2A=4,即A=2.?
又點A(1,3[]2)在橢圓上,因此![]() +
+![]() =1,b2=3.??
=1,b2=3.??
∴C2=A2-b2=1.?
∴橢圓C的方程為![]() =1,焦點F1(-1,0),F2(1,0).??
=1,焦點F1(-1,0),F2(1,0).??
(2)設橢圓C上的動點為K(x,y),線段F1K的中點Q(x,y)滿足:x=![]() ,y=
,y=![]() ,
,
∴x1=2x+1,y1=2y.?
∴![]() =1,即(x+
=1,即(x+![]() )2+
)2+![]() =1為所求的軌跡方程.?
=1為所求的軌跡方程.?
(3)類似的性質為:若M、N是雙曲線![]() =1上關于原點對稱的兩個點,點P是雙曲線上任意一點,當直線PM、PN的斜率都存在,并記為kPM、kPN時,那么kPM與kPN之積是與點P位置無關的定值.設點M的坐標為(M,n),則點N的坐標為(-M,-n),其中
=1上關于原點對稱的兩個點,點P是雙曲線上任意一點,當直線PM、PN的斜率都存在,并記為kPM、kPN時,那么kPM與kPN之積是與點P位置無關的定值.設點M的坐標為(M,n),則點N的坐標為(-M,-n),其中![]() =1.
=1.
又設點P的坐標為(x,y),由kPM=![]() ,?
,?
kPN=![]() 得kPM·kPN=
得kPM·kPN=![]() ·
·![]() =
=![]() .?
.?
將y2=![]() x2-b2,n2=
x2-b2,n2=![]() M2-b2代入,得kPM·kPN=
M2-b2代入,得kPM·kPN=![]()


科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 (a>b>0)的左、右兩個焦點,橢圓C上的點
(a>b>0)的左、右兩個焦點,橢圓C上的點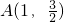 到兩點的距離之和等于4.
到兩點的距離之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com