Question

如圖，在四棱錐P―ABCD中，平面PAB⊥平面ABCD，底面ABCD是邊長為2的正方形，△PAB為等邊三角形.

   （1）求PC與平面ABCD所成角的大小；

   （2）求二面角B―AC―P的大小；

   （3）求點A到平面PCD的距離.

Answer 1

解法一：

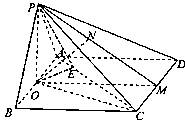
   （1）解：設O為AB中點，連結PO，CO，∵PA=PB，∴PO⊥AB.

又平面PAB⊥平面ABCD，且交線為AB，∴PO⊥平面ABCD.

∴∠PCO為直線PC與平面ABCD所成的角.

由底面正方形邊長為2，△PAB為等邊三角形，可得PO=，CO=

∴

∴PC與平面ABCD所成的角大小為

   （2）解：過O做OE⊥AC，垂足為E，連結PE.

∵PO⊥平面ABCD，則三垂線定理，可知PE⊥AC，

∴∠PEO為二面角B―AC―P的平面角.

可求得OE=. 又PO= ∴

∴二面角P―AC―B的大小為

   （3）解：∵AB∥平面PCD，∴點A到平面PCD的距離等于點O到平面PCD的距離.

取CD中點M，連結OM，PM，∵PO⊥CD，OM⊥CD，∴CD⊥平面POM.

∴平面POM⊥平面PCD. 過O做ON⊥PM，垂足為N，則ON⊥平面PCD.

在△POM中，PO=，OM=2，可得PM=，

∴點A到平面PCD的距離為

解法二：

   （1）解：同解法一

   （2）解：建立如圖的空間直角坐標系O―xyz，

則A（－1，0，0），B（1，0，0），則P（0，0，），C（1，2，0）

       設為平面PAC的一個法向量，

       則

       又

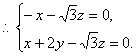    令z=1，得

       得

       又是平面ABC的一個法向量，

       設二面角B―AC―P的大小為，

則

 

   （3）解：設為平面PCD的一個法向量.

       則 由D（－1，2，0），可知），

       可得a=0，令，則c=2.

       得，

       設點A到平面PCD的距離為d，則

       ∴點A到平面PCD的距離為