
分析 (1)根據題意,分析可得$\sqrt{(x-\sqrt{2})^{2}+{y}^{2}}$+$\sqrt{(x+\sqrt{2})^{2}+{y}^{2}}$=2$\sqrt{3}$,由橢圓的定義可得點P(x,y)對應的曲線方程C是橢圓,進而由題意可得a、c的值,計算可得b的值,代入橢圓的標準方程即可得答案;
(2)根據題意,分2種情況討論:、①當直線l的斜率不存在時,直線l的方程為x=1,代入橢圓的方程可得A,B兩點的坐標,計算可得k1+k2的值,②當直線l的斜率存在時,設直線l的方程為y=k(x-1),聯立直線與橢圓的方程,可得(3k2+1)x2-6k2x+3k2-3=0.由根與系數的關系分析可得x1+x2=$\frac{6{k}^{2}}{3{k}^{2}+1}$,x1x2=$\frac{3{k}^{2}-3}{3{k}^{2}+1}$.結合直線的方程可得k1+k2═$\frac{2-{y}_{1}}{3-{x}_{1}}$+$\frac{2-{y}_{2}}{3-{x}_{2}}$,將其變形化簡可得k1+k2的值,綜合2種情況即可得答案.
解答 解:(1)、依題意:三個數$\sqrt{(x-\sqrt{2})^{2}+{y}^{2}}$,$\sqrt{3}$,$\sqrt{(x+\sqrt{2})^{2}+{y}^{2}}$成等差數列,
則有$\sqrt{(x-\sqrt{2})^{2}+{y}^{2}}$+$\sqrt{(x+\sqrt{2})^{2}+{y}^{2}}$=2$\sqrt{3}$,
所以點P(x,y)對應的曲線方程C是橢圓,
得$\left\{\begin{array}{l}{a=\sqrt{3}}\\{c=\sqrt{2}}\end{array}\right.$.
故b=1
橢圓C方程為$\frac{{x}^{2}}{3}$+y2=1,
(2)、①當直線l的斜率不存在時,直線l的方程為x=1.由$\left\{\begin{array}{l}{x=1}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$解得$\left\{\begin{array}{l}x=1\\ y=±\frac{\sqrt{6}}{3}.\end{array}$
不妨設A(1,$\frac{\sqrt{6}}{3}$),B(1,-$\frac{\sqrt{6}}{3}$),
因為k1+k2=2,
②當直線l的斜率存在時,設直線l的方程為y=k(x-1).
將y=k(x-1)代入$\frac{{x}^{2}}{3}$+y2=1,
整理得(3k2+1)x2-6k2x+3k2-3=0.
設A(x1,y1),B(x2,y2),則x1+x2=$\frac{6{k}^{2}}{3{k}^{2}+1}$,x1x2=$\frac{3{k}^{2}-3}{3{k}^{2}+1}$.
又y1=k(x1-1),y2=k(x2-1),
所以k1+k2=$\frac{2-{y}_{1}}{3-{x}_{1}}$+$\frac{2-{y}_{2}}{3-{x}_{2}}$
=$\frac{(2-{y}_{1})(3-{x}_{2})+(2-{y}_{2})(3-{x}_{1})}{(3-{x}_{1})(3-{x}_{2})}$
=$\frac{[2-k({x}_{1}-1)](3-{x}_{2})+[2-k({x}_{2}-1)](3-{x}_{1})}{{x}_{1}{x}_{2}-3({x}_{1}+{x}_{2})+9}$
=$\frac{2(12{k}^{2}+6)}{12{k}^{2}+6}$=2
即k1+k2=2,
綜合可得:其k1+k2值為定植為2.
點評 本題考查橢圓與直線的位置關系,涉及橢圓的定義以及標準方程,(2)中不能忽略直線斜率不存在的情況.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
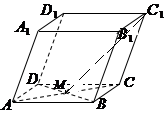 四棱柱ABCD-A1B1C1D1的底面是平行四邊形,M是AC與BD的交點.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,則$\overrightarrow{{C_1}M}$可以表示為( )
四棱柱ABCD-A1B1C1D1的底面是平行四邊形,M是AC與BD的交點.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,則$\overrightarrow{{C_1}M}$可以表示為( )| A. | $\overrightarrow a+\overrightarrow b+\frac{1}{2}\overrightarrow c$ | B. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {0,1,8,10} | B. | {1,2,4,6} | C. | {0,8,10} | D. | ∅ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com