
【題目】函數f(x)=5 ![]() +
+ ![]() 的定義域為( )
的定義域為( )
A.{x|1<x≤2}
B.{x|1≤x≤2}
C.{x|x≤2且x≠1}
D.{x|x≥0且x≠1}
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}滿足a3=2,前3項和為S3=![]() .
.
(1)求{an}的通項公式;
(2)設等比數列{bn}滿足b1=a1,b4=a15,求{bn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某職稱晉級評定機構對參加某次專業技術考試的100人的成績進行了統計,繪制了頻率分布直方圖(如圖所示),規定80分及以上者晉級成功,否則晉級失敗(滿分為100分).
晉級成功 | 晉級失敗 | 合計 | |
男 | 16 | ||
女 | 50 | ||
合計 |
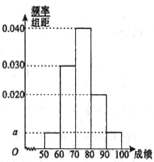
(Ⅰ)求圖中![]() 的值;
的值;
(Ⅱ)根據已知條件完成下面![]() 列聯表,并判斷能否有85%的把握認為“晉級成功”與性別有關?
列聯表,并判斷能否有85%的把握認為“晉級成功”與性別有關?
(Ⅲ)將頻率視為概率,從本次考試的所有人員中,隨機抽取4人進行約談,記這4人中晉級失敗的人數為![]() ,求
,求![]() 的分布列與數學期望
的分布列與數學期望![]() .
.
(參考公式:![]() ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2015高考湖北(理)20】某廠用鮮牛奶在某臺設備上生產![]() 兩種奶制品.生產1噸
兩種奶制品.生產1噸![]() 產品需鮮牛奶2噸,使用設備1小時,獲利1000元;生產1噸
產品需鮮牛奶2噸,使用設備1小時,獲利1000元;生產1噸![]() 產品需鮮牛奶1.5噸,使用設備1.5小時,獲利1200元.要求每天
產品需鮮牛奶1.5噸,使用設備1.5小時,獲利1200元.要求每天![]() 產品的產量不超過
產品的產量不超過![]() 產品產量的2倍,設備每天生產
產品產量的2倍,設備每天生產![]() 兩種產品時間之和不超過12小時. 假定每天可獲取的鮮牛奶數量W(單位:噸)是一個隨機變量,其分布列為
兩種產品時間之和不超過12小時. 假定每天可獲取的鮮牛奶數量W(單位:噸)是一個隨機變量,其分布列為
W | 12 | 15 | 18 |
P | 0.3 | 0.5 | 0.2 |
該廠每天根據獲取的鮮牛奶數量安排生產,使其獲利最大,因此每天的最大獲利![]() (單位:元)是一個隨機變量.
(單位:元)是一個隨機變量.
(Ⅰ)求![]() 的分布列和均值;
的分布列和均值;
(Ⅱ) 若每天可獲取的鮮牛奶數量相互獨立,求3天中至少有1天的最大獲利超過10000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)在區間[a,b]上的圖象是連續不斷的一條曲線,有下列說法:
①若f(a)f(b)>0,則函數y=f(x)在區間(a,b)上沒有零點;
②若f(a)f(b)>0,則函數y=f(x)在區間(a,b)上可能有零點;
③若f(a)f(b)<0,則函數y=f(x)在區間(a,b)上沒有零點;
④若f(a)f(b)<0,則函數y=f(x)在區間(a,b)上至少有一個零點;
其中正確說法的序號是(把所有正確說法的序號都填上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點![]() 到點
到點![]() 和直線l:
和直線l: ![]() 的距離相等.
的距離相等.
(Ⅰ)求動點![]() 的軌跡E的方程;
的軌跡E的方程;
(Ⅱ)已知不與![]() 垂直的直線
垂直的直線![]() 與曲線E有唯一公共點A,且與直線
與曲線E有唯一公共點A,且與直線![]() 的交點為
的交點為![]() ,以AP為直徑作圓
,以AP為直徑作圓![]() .判斷點
.判斷點![]() 和圓
和圓![]() 的位置關系,并證明你的結論.
的位置關系,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國Ⅳ標準規定:輕型汽車的屢氧化物排放量不得超過80mg/km.根據這個標準,檢測單位從某出租車公司運營的A、B兩種型號的出租車中分別抽取5輛,對其氮氧化物的排放量進行檢測,檢測結果記錄如表(單位:mg/km)
A | 85 | 80 | 85 | 60 | 90 |
B | 70 | x | 95 | y | 75 |
由于表格被污損,數據x,y看不清,統計員只記得A、B兩種出租車的氮氧化物排放量的平均值相等,方差也相等.
(1)求表格中x與y的值;
(2)從被檢測的5輛B種型號的出租車中任取2輛,記“氮氧化物排放量超過80mg/km”的車輛數為X,求X=1時的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com