
已知 .
.
(1)若 恒成立,求
恒成立,求 的最大值;
的最大值;
(2)若 為常數,且
為常數,且 ,記
,記 ,求
,求 的最小值.
的最小值.
(1)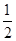 ;(2)
;(2)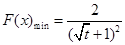 .
.
解析試題分析:本題考查導數與函數及運用導數求單調區間、最值等數學知識,突出考查運用數學知識和方法分析問題解決問題的能力.第一問,是恒成立問題,先將恒成立問題轉化為最值問題,求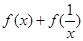 的最值是本問的關鍵,法一,利用基本不等式求最值,法二,利用導數求最值,無論用哪種方法都應注意函數的定義域;第二問,令
的最值是本問的關鍵,法一,利用基本不等式求最值,法二,利用導數求最值,無論用哪種方法都應注意函數的定義域;第二問,令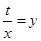 ,將
,將 進行轉化,化簡成
進行轉化,化簡成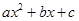 的形式,利用二次函數的單調性求
的形式,利用二次函數的單調性求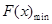 .
.
試題解析:(1)(解法一)
設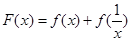
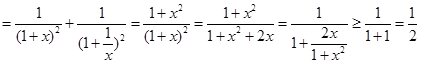 ,
,
∴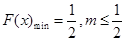 ,∴
,∴ 的最大值為
的最大值為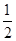 .
.
(解法二)設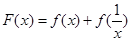
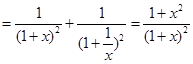 ,
,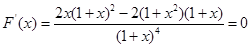 ,
,
∴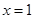 ,當
,當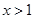 時,
時,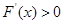 ,當
,當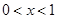 時,
時,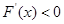 ,∴
,∴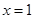 為極小值點,
為極小值點,
∴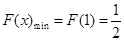 ,∴
,∴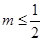 ,∴
,∴ 的最大值為
的最大值為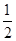 .
.
(2)設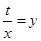 ,則
,則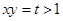 ,則
,則
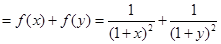
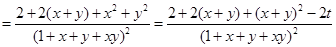
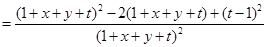
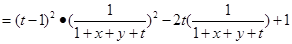
令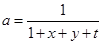 ,則
,則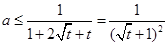
即 ,
,
設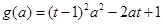 ,∵
,∵ 其對稱軸
其對稱軸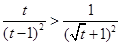 ,
, 在
在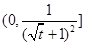 上單調遞減,∴
上單調遞減,∴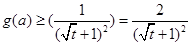 ,
,
∴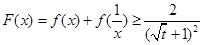 ,
,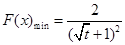 .
.
考點:1.恒成立問題;2.基本不等式;3.利用導數求函數的單調區間和最值;4.二次函數的單調性和最值.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:解答題
某地開發了一個旅游景點,第1年的游客約為100萬人,第2年的游客約為120萬人.某數學興趣小組綜合各種因素預測:①該景點每年的游客人數會逐年增加;②該景點每年的游客都達不到130萬人.該興趣小組想找一個函數 來擬合該景點對外開放的第
來擬合該景點對外開放的第
 年與當年的游客人數
年與當年的游客人數 (單位:萬人)之間的關系.
(單位:萬人)之間的關系.
(1)根據上述兩點預測,請用數學語言描述函數 所具有的性質;
所具有的性質;
(2)若 =
= ,試確定
,試確定 的值,并考察該函數是否符合上述兩點預測;
的值,并考察該函數是否符合上述兩點預測;
(3)若 =
= ,欲使得該函數符合上述兩點預測,試確定
,欲使得該函數符合上述兩點預測,試確定 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com