
【題目】如圖,![]() 是東西方向的公路北側的邊緣線,某公司準備在
是東西方向的公路北側的邊緣線,某公司準備在![]() 上的一點
上的一點![]() 的正北方向的
的正北方向的![]() 處建設一倉庫,設
處建設一倉庫,設![]() ,并在公路北側建造邊長為
,并在公路北側建造邊長為![]() 的正方形無頂中轉站
的正方形無頂中轉站![]() (其中
(其中![]() 在
在![]() 上),現從倉庫
上),現從倉庫![]() 向
向![]() 和中轉站分別修兩條道路
和中轉站分別修兩條道路![]() ,已知
,已知![]() ,且
,且![]() .
.

(1)求![]() 關于
關于![]() 的函數解析式,并求出定義域;
的函數解析式,并求出定義域;
(2)如果中轉站四堵圍墻造價為10萬元![]() ,兩條道路造價為30萬元
,兩條道路造價為30萬元![]() ,問:
,問:![]() 取何值時,該公司建設中轉站圍墻和兩條道路總造價
取何值時,該公司建設中轉站圍墻和兩條道路總造價![]() 最低.
最低.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)在△BCF中,CF=x,∠FBC=30°,CF⊥BF,BC=2x.在△ABC中,AB=y,AC=y-1,∠ABC=60°,由余弦定理,求解函數的解析式,然后求解定義域.(2)求出M=30(2y-1)+40x,通過基本不等式求解表達式的最值即可.
(1)在△BCF中,CF=x,∠FBC=30°,CF⊥BF,所以BC=2x.
在△ABC中,AB=y,AC=y﹣1,∠ABC=60°,
由余弦定理,得AC2=BA2+BC2﹣2BABCcos∠ABC,
即 (y﹣1)2=y2+(2x)2﹣2y2xcos60°,
所以 ![]() .
.
由AB﹣AC<BC,得![]() .又因為
.又因為![]() >0,所以x>1.
>0,所以x>1.
所以函數![]() 的定義域是(1,+∞).
的定義域是(1,+∞).
(2)M=30(2y﹣1)+40x.
因為![]() .(x>1),所以M=30
.(x>1),所以M=30![]()
即 M=10![]() .
.
令t=x﹣1,則t>0.于是M(t)=10(16t+![]() ),t>0,由基本不等式得M(t)≥10(2
),t>0,由基本不等式得M(t)≥10(2![]() )=490,
)=490,
當且僅當t=![]() ,即x=
,即x=![]() 時取等號.
時取等號.
答:當x=![]() km時,公司建中轉站圍墻和兩條道路最低總造價M為490萬元.
km時,公司建中轉站圍墻和兩條道路最低總造價M為490萬元.


科目:高中數學 來源: 題型:
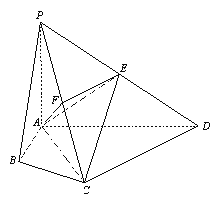
【題目】(14分)在四棱錐P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E為PD的中點,PA=2AB=2.
(Ⅰ)求四棱錐P-ABCD的體積V;
(Ⅱ)若F為PC的中點,求證PC⊥平面AEF;
(Ⅲ)求證CE∥平面PAB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在直角梯形![]() 中,AB∥CD,
中,AB∥CD,![]() ,且
,且![]() .現以
.現以![]() 為一邊向梯形外作正方形
為一邊向梯形外作正方形![]() ,然后沿邊
,然后沿邊![]() 將正方形
將正方形![]() 翻折,使平面
翻折,使平面![]() 與平面
與平面![]() 垂直,如圖2.
垂直,如圖2.


(Ⅰ)求證:BC⊥平面DBE;
(Ⅱ)求點D到平面BEC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過點A(0,2)的直線![]() 與橢圓C:
與橢圓C:![]() 交于P,Q兩點.
交于P,Q兩點.
(1)若直線![]() 的斜率為k,求k的取值范圍;
的斜率為k,求k的取值范圍;
(2)若以PQ為直徑的圓經過點E(1,0),求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知極坐標系的極點與直角坐標系的原點重合,極軸與直角坐標系中x軸的正半軸重合,若曲線C的參數方程為 ![]() (α是參數),直線l的極坐標方程為
(α是參數),直線l的極坐標方程為 ![]() ρsin(θ﹣
ρsin(θ﹣ ![]() )=1.
)=1.
(1)將曲線C的參數方程化為極坐標方程;
(2)由直線l上一點向曲線C引切線,求切線長的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一般情況下,城市主干道上的車流速度 ![]() (單位:千米/小時)是車流密度
(單位:千米/小時)是車流密度 ![]() (單位:輛/千米)的函數。當主干道上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0千米/小時;當車流密度不超過20輛/千米時,車流速度為60千米/小時。研究表明:當
(單位:輛/千米)的函數。當主干道上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0千米/小時;當車流密度不超過20輛/千米時,車流速度為60千米/小時。研究表明:當 ![]() 時,車流速度
時,車流速度 ![]() 是車流密度
是車流密度 ![]() 的一次函數。
的一次函數。
(1)當 ![]() 時,求函數
時,求函數 ![]() 的表達式;
的表達式;
(2)當車流密度為多大時,車流量(單位時間內通過主干道上某觀測點的車輛數,單位:輛/小時) ![]() 可以達到最大?并求出最大值。(精確到1輛/小時)
可以達到最大?并求出最大值。(精確到1輛/小時)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a≥3,函數F(x)=min{2|x﹣1|,x2﹣2ax+4a﹣2},其中min(p,q)= ![]()
(1)求使得等式F(x)=x2﹣2ax+4a﹣2成立的x的取值范圍
(2)(1)求F(x)的最小值m(a)
(3)求F(x)在[0,6]上的最大值M(a)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com