
【題目】平面直角坐標系![]() 中,圓M與y軸相切,并且經過點
中,圓M與y軸相切,并且經過點![]() ,
,![]() .
.
(1)求圓M的方程;
(2)過點![]() 作圓M的兩條互垂直的弦AC、BD,求四邊形ABCD面積的最大值.
作圓M的兩條互垂直的弦AC、BD,求四邊形ABCD面積的最大值.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖1,點![]() 為正方形
為正方形![]() 邊
邊![]() 上異于點
上異于點![]() 的動點,將
的動點,將![]() 沿
沿![]() 翻折,得到如圖2所示的四棱錐
翻折,得到如圖2所示的四棱錐![]() ,且平面
,且平面![]() 平面
平面![]() ,點
,點![]() 為線段
為線段![]() 上異于點
上異于點![]() 的動點,則在四棱錐
的動點,則在四棱錐![]() 中,下列說法正確的有( )
中,下列說法正確的有( )

A. 直線![]() 與直線
與直線![]() 必不在同一平面上
必不在同一平面上
B. 存在點![]() 使得直線
使得直線![]() 平面
平面![]()
C. 存在點![]() 使得直線
使得直線![]() 與平面
與平面![]() 平行
平行
D. 存在點![]() 使得直線
使得直線![]() 與直線
與直線![]() 垂直
垂直
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f (x)=x2,g(x)=x-1.
(1)若存在x∈R使f(x)<b·g(x),求實數b的取值范圍;
(2)設F(x)=f(x)-mg(x)+1-m-m2,且|F(x)|在![]() 上單調遞增,求實數m的取值范圍.
上單調遞增,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() 集合
集合![]() ,集合
,集合![]() ,且集合D滿足
,且集合D滿足![]() .
.
(1)求實數a的值.
(2)對集合![]() ,其中
,其中![]() ,定義由
,定義由![]() 中的元素構成兩個相應的集合:
中的元素構成兩個相應的集合:![]() ,
,![]() ,其中
,其中![]() 是有序實數對,集合S和T中的元素個數分別為
是有序實數對,集合S和T中的元素個數分別為![]() 和
和![]() ,若對任意的
,若對任意的![]() ,總有
,總有![]() ,則稱集合
,則稱集合![]() 具有性質P.
具有性質P.
①請檢驗集合![]() 是否具有性質P,并對其中具有性質P的集合,寫出相應的集合S和T.
是否具有性質P,并對其中具有性質P的集合,寫出相應的集合S和T.
②試判斷m和n的大小關系,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設p:實數x滿足x2-5ax+4a2<0(其中a>0),q:實數x滿足2<x≤5.
(1)若a=1,且p∧q為真,求實數x的取值范圍;
(2)若![]() q是
q是![]() p的必要不充分條件,求實數a的取值范圍.
p的必要不充分條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某地每單位面積菜地年平均使用氮肥量x(單位:kg)與每單位面積蔬菜年平均產量Y(單位:t)之間的關系有如下數據:
年份 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
x/kg | 70 | 74 | 80 | 78 | 85 | 92 | 90 | 95 |
Y/t | 5.1 | 6.0 | 6.8 | 7.8 | 9.0 | 10.2 | 10.0 | 12.0 |
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
x/kg | 92 | 108 | 115 | 123 | 130 | 138 | 145 | |
Y/t | 11.5 | 11.0 | 11.8 | 12.2 | 12.5 | 12.8 | 13.0 |
(1)求x與Y之間的相關系數,并檢驗是否線性相關;
(2)若線性相關,求每單位面積蔬菜年平均產量Y與每單位面積菜地年平均使用氮肥量x之間的回歸直線方程,并估計每單位面積菜地年平均使用氮肥150 kg時,每單位面積蔬菜的年平均產量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:y=(x+1)2與圓 ![]() (r>0)有一個公共點A,且在A處兩曲線的切線為同一直線l.
(r>0)有一個公共點A,且在A處兩曲線的切線為同一直線l.
(1)求r;
(2)設m,n是異于l且與C及M都相切的兩條直線,m,n的交點為D,求D到l的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合M={x|x<-3,或x>5},P={x|(x-a)·(x-8)≤0}.
(1)求M∩P={x|5<x≤8}的充要條件;
(2)求實數a的一個值,使它成為M∩P={x|5<x≤8}的一個充分但不必要條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱柱ABC﹣A1B1C1中,已知AB=AC=AA1= ![]() ,BC=4,點A1在底面ABC的投影是線段BC的中點O.
,BC=4,點A1在底面ABC的投影是線段BC的中點O. 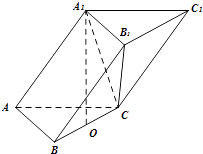
(1)證明在側棱AA1上存在一點E,使得OE⊥平面BB1C1C,并求出AE的長;
(2)求平面A1B1C與平面BB1C1C夾角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com