
如圖所示,在五面體P-ABCD中,底面ABCD是平行四邊形,∠BAD=60°,AB=4,AD=2,PB=![]() ,PD=
,PD=![]() .
.
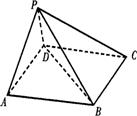
(1)求證:BD⊥平面PAD;
(2)若PD與底面ABCD成60°的角,試求二面角P-BC-A的大小.
|
(1)由已知AB=4,AD=2,∠BAD=60°, 得BD2=AD2+AB2-2AD·ABcos60°=4+16-2×2×4× ∴△ABD是直角三角形,∠ADB=90°,即AD⊥BD. 3分 在△PDB中,PD= ∴PB2=PD2+BD2,故得PD⊥BD. 又PD∩AD=D,∴BD⊥平面PAD. 6分 (2)∵BD⊥平面PAD,BD ∴平面PAD⊥平面ABCD. 8分 作PE⊥AD于E,又PE ∴∠PDE是PD與底面BCD所成的角,∴∠PDE=60°, 作EF⊥BC于F,連PF,則PF⊥BC,∴∠PFE是二面角P-BC-A的平面角. 又EF=BD= 故二面角P-BC-A的大小為arctan |


 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案 陽光課堂同步練習系列答案
陽光課堂同步練習系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com