Question

如圖所示，直三棱柱ABC—A₁B₁C₁中，底面是以∠ABC為直角的等腰直角三角形，AC=2a,BB₁=3a,D為A₁C₁的中點，E為B₁C的中點,

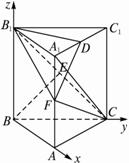
(1)求直線BE與A₁C所成的角的余弦值.

(2)在線段AA₁上是否存在點F，使CF⊥平面B₁DF？若存在，求出|AF|；若不存在，請說明?理由.

 

Answer 1

解析：(1)以B為原點，建立如圖所示的空間直角坐標系.?

∵AC=2a,∠ABC=90°,

∴AB=BC=a.

∴B(0,0,0),C(0, a,0),A(a,0,0),A₁(a,0,3a),C₁(0, a,3a),B₁(0,0,3a).

∴D(a, a,3a),E(0,a,a).?

∴=(a,-a,3a),=(0,a,a).

∴||=a,||=a.

∴·=0-a²+a²=a².?

∴cosθ==.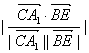

(2)假設存在點F，要使⊥平面B₁DF，只要⊥且⊥.

不妨設AF=b,則F(a,0,b),=(a,-a,b), =(a,0,b-3a), =(a,a,0).

∵·=a²-a²=0,?

∴⊥恒成立.?

·=2a²+b(b-3a)=0b=a或b=2a,故當||=a或2a時，⊥平面B₁DF.