
【題目】某城市隨機抽取一年內100 天的空氣質量指數(AQI)的監測數據,結果統計如表:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,300] | >300 |
空氣質量 | 優 | 良 | 輕度污染 | 輕度污染 | 中度污染 | 重度污染 |
天數 | 6 | 14 | 18 | 27 | 20 | 15 |
(1)若本次抽取的樣本數據有30 天是在供暖季,其中有8 天為嚴重污染.根據提
供的統計數據,完成下面的2×2 列聯表,并判斷是否有95%的把握認為“該城市本年的
空氣嚴重污染與供暖有關”?
非重度污染 | 嚴重污染 | 合計 | |
供暖季 | |||
非供暖季 | |||
合計 | 100 |
(2)已知某企業每天的經濟損失y(單位:元)與空氣質量指數x 的關系式為y=  試估計該企業一個月(按30 天計算)的經濟損失的數學期望.
試估計該企業一個月(按30 天計算)的經濟損失的數學期望.
參考公式:K2= ![]()
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【答案】
(1)解:根據題設中的數據得到如下2×2列聯表:
非嚴重污染 | 嚴重污染 | 總計 | |
供暖季 | 22 | 8 | 30 |
非供暖季 | 63 | 7 | 70 |
總計 | 85 | 15 | 100 |
將2×2列聯表中的數據代入公式計算,得:
K2= ![]() ≈4.575.
≈4.575.
∵4.575>3.841
∴由95%的把握認為:“該城市本年的空氣嚴重污染與供暖有關”
(2)解:任選一天,設該天的經濟損失為X元,則:
P(X=0)=P(0≤x≤100)= ![]()
P(X=400)=P(100<x≤300)= ![]() ,
,
P(X=2000)=P(x>300)= ![]()
∴E(X)=0× ![]() +400×
+400× ![]() +2000×
+2000× ![]() =560.
=560.
∴該企業一個月(按30 天計算)的經濟損失的數學期望為30×E(X)=16800元.
【解析】(1)列出2×2列聯表,由公式,得到結果.(2)由分段函數,得到各段的概率,由此得到數學期望.


科目:高中數學 來源: 題型:
【題目】小麗今天晚自習準備復習歷史、地理或政治中的一科,她用數學游戲的結果來決定選哪一科,游戲規則是:在平面直角坐標系中,以原點![]() 為起點,再分別以
為起點,再分別以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 這5個點為終點,得到5個向量,任取其中兩個向量,計算這兩個向量的數量積
這5個點為終點,得到5個向量,任取其中兩個向量,計算這兩個向量的數量積![]() ,若
,若![]() ,就復習歷史,若
,就復習歷史,若![]() ,就復習地理,若
,就復習地理,若![]() ,就復習政治.
,就復習政治.
(1)寫出![]() 的所有可能取值;
的所有可能取值;
(2)求小麗復習歷史的概率和復習地理的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過曲線y=x2(x≥0)上某一點A作一切線l,使之與曲線以及x軸所圍成的圖形的面積為 ![]() ,試求:
,試求:
(1)切點A的坐標;
(2)過切點A的切線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2. 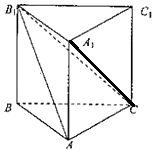
(1)求證:平面B1AC⊥平面ABB1A1;
(2)求直線A1C與平面B1AC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海中一小島![]() 的周圍
的周圍![]()
![]() 內有暗礁,海輪由西向東航行至
內有暗礁,海輪由西向東航行至![]() 處測得小島
處測得小島![]() 位于北偏東
位于北偏東![]() ,航行8
,航行8![]() 后,于
后,于![]() 處測得小島
處測得小島![]() 在北偏東
在北偏東![]() (如圖所示).
(如圖所示).

(1)如果這艘海輪不改變航向,有沒有觸礁的危險?請說明理由.
(2)如果有觸礁的危險,這艘海輪在![]() 處改變航向為東偏南
處改變航向為東偏南![]() (
(![]() )方向航行,求
)方向航行,求![]() 的最小值.
的最小值.
附: ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司今年年初用25萬元引進一種新的設備,投入設備后每年收益為21萬元.該公司第n年需要付出設備的維修和工人工資等費用an的信息如圖. 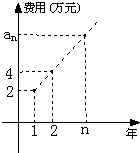
(1)求an;
(2)引進這種設備后,第幾年后該公司開始獲利;
(3)這種設備使用多少年,該公司的年平均獲利最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com