【題目】已知函數
.
(I)當a=-1時，
①求曲線y= f(x)在點(0，f(0))處的切線方程；
②求函數f(x)的最小值；
(II)求證:當
時，曲線
與
有且只有一個交點.
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
,
，其焦距為
，點E為橢圓的上頂點，且
．
（1）求橢圓C的方程；
（2）設圓
的切線l交橢圓C于A，B兩點（O為坐標原點），求證
；
（3）在（2）的條件下，求
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】春節期間爆發的新型冠狀病毒（COVID-19）是新中國成立以來感染人數最多的一次疫情.一個不知道自己已感染但處于潛伏期的甲從疫區回到某市過春節，回到家鄉后與朋友乙、丙、丁相聚過，最終乙、丙、丁也感染了新冠病毒.可以肯定的是乙受甲感染的，丙是受甲或乙感染的，假設他受甲和受乙感染的概率分別是
和
.丁是受甲、乙或丙感染的，假設他受甲、乙和丙感染的概率分別是
、和.在這種假設之下，乙、丙、丁中直接受甲感染的人數為
.
（1）求的分布列和數學期望；
（2）該市在發現在本地出現新冠病毒感染者后，迅速采取應急措施，其中一項措施是各區必須每天及時，上報新增疑似病例人數.
區上報的連續
天新增疑似病例數據是“總體均值為
，中位數
”，
區上報的連續天新增疑似病例數據是“總體均值為
，總體方差為”.設區和區連續天上報新增疑似病例人數分別為
和
，
和
分別表示區和區第
天上報新增疑似病例人數（和
均為非負）.記
，
.
①試比較
和
的大小；
②求和中較小的那個字母所對應的個數有多少組？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在三棱柱ABC﹣A1B1C1中，M，M1分別為AB，A1B1中點.
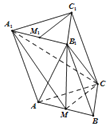
（1）求證：C1M1∥面A1MC；
（2）若面ABC⊥面ABB1A1，△AB1B為正三角形，AB＝2，BC＝1，
，求四棱錐B1﹣AA1C1C的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（1）若函數
在
，
上單調遞增，求實數
的取值范圍；
（2）若函數在
處的切線平行于
軸，是否存在整數
，使不等式
在
時恒成立？若存在，求出的最大值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】大自然是非常奇妙的，比如蜜蜂建造的蜂房.蜂房的結構如圖所示，開口為正六邊形ABCDEF，側棱AA'、BB'、CC'、DD'、EE'、FF'相互平行且與平面ABCDEF垂直，蜂房底部由三個全等的菱形構成.瑞士數學家克尼格利用微積分的方法證明了蜂房的這種結構是在相同容積下所用材料最省的，因此，有人說蜜蜂比人類更明白如何用數學方法設計自己的家園.英國數學家麥克勞林通過計算得到∠B′C′D′＝109°28′16'.已知一個房中BB'＝5
，AB＝2
，tan54°44′08'
，則此蜂房的表面積是_____.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）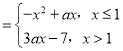
，若存在x1，x2∈R且x1≠x2，使得f（x1）＝f（x2）成立，則實數a的取值范圍是（ ）
A.[3，+∞）B.（3，+∞）C.（﹣∞，3）D.（﹣∞，3]
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在抗擊新冠肺炎疫情期間，很多人積極參與了疫情防控的志愿者活動.各社區志愿者服務類型有：現場值班值守，社區消毒，遠程教育宣傳，心理咨詢（每個志愿者僅參與一類服務）.參與A，B，C三個社區的志愿者服務情況如下表：
社區 | 社區服務總人數 | 服務類型 | |||
現場值班值守 | 社區消毒 | 遠程教育宣傳 | 心理咨詢 | ||
A | 100 | 30 | 30 | 20 | 20 |
B | 120 | 40 | 35 | 20 | 25 |
C | 150 | 50 | 40 | 30 | 30 |
（1）從上表三個社區的志愿者中任取1人，求此人來自于A社區，并且參與社區消毒工作的概率；
（2）從上表三個社區的志愿者中各任取1人調查情況，以X表示負責現場值班值守的人數，求X的分布列；
（3）已知A社區心理咨詢滿意率為0.85，B社區心理咨詢滿意率為0.95，C社區心理咨詢滿意率為0.9，“
，
，
”分別表示A，B，C社區的人們對心理咨詢滿意，“
，
，
”分別表示A，B，C社區的人們對心理咨詢不滿意，寫出方差
，
，
的大小關系.（只需寫出結論）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
