
【題目】如圖,四邊形ABCD為矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于點F,且點F在CE上. 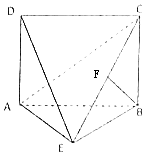
(1)求證:AE⊥BE;
(2)求三棱錐C﹣ADE的體積.
【答案】
(1)證明:∵DA⊥平面ABE,BC∥DA,
∴BC⊥平面ABE,
∵AE平面ABE,∴AE⊥BC,
∵BF⊥平面ACE于點F,AE平面ACE,
∴AE⊥BF,
∵BC∩BF=B,
BC平面BEC,BF平面BEC,∴AE⊥平面BEC,
∵BE平面BEC,∴AE⊥BE
(2)解:作EH⊥AB,
∵DA⊥平面ABE,EH平面ABE,∴AD⊥EH,
AD∩AB=A,AD平面ABCD,AB平面ABCD,
∴EH⊥平面ABCD,
由(1)得AE⊥BE,AE=EB=BC=2,
AB=2 ![]() ,EH=
,EH= ![]() ,
,
∴三棱錐C﹣ADE的體積VC﹣ADE=VE﹣ACD= ![]() =
= ![]() =
= ![]() .
.

【解析】(1)推導出BC⊥平面ABE,從而AE⊥BC,再求出AE⊥BF,從而AE⊥平面BEC,由此能證明AE⊥BE.(2)作EH⊥AB,三棱錐C﹣ADE的體積VC﹣ADE=VE﹣ACD , 由此能求出結果.
【考點精析】關于本題考查的直線與平面垂直的性質,需要了解垂直于同一個平面的兩條直線平行才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】已知數列{an}是公差不為零的等差數列,a1=1,且a2 , a4 , a8成等比數列.
(1)求數列{an}的通項公式;
(2)設數列{bn}滿足:a1b1+a2b2+a3b3+…+anbn=2n+1 , n∈N* , 令cn= ![]() ,n∈N* , 求數列{cncn+1}的前n項和Sn .
,n∈N* , 求數列{cncn+1}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市要對兩千多名出租車司機的年齡進行調查,現從中隨機抽出100名司機,已知抽到的司機年齡都在[20,45)歲之間,根據調查結果得出司機的年齡情況殘缺的頻率分布直方圖如圖所示,利用這個殘缺的頻率分布直方圖估計該市出租車司機年齡的中位數大約是歲. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為選拔選手參加“中國謎語大會”,某中學舉行了一次“謎語大賽”活動,為了了解本次競賽學生的成績情況,從中抽取了部分學生的分數(得分取正整數,滿分為100分)作為樣本,(樣本容量為![]() )進行統計.按照
)進行統計.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分組作出如下頻率分布直方圖.
的分組作出如下頻率分布直方圖.
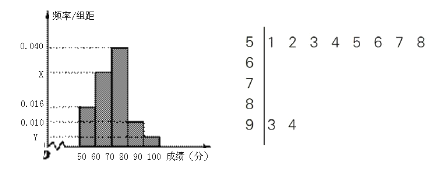
(1)由如下莖葉圖(圖中僅列出了得分在![]() ,
,![]() 的數據)提供的信息,求樣本容量
的數據)提供的信息,求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 的值;
的值;
(2)在選取的樣本中,從競賽成績在80分以上(含80分)的學生中隨機抽取2名學生參加“中國謎語大會”,求所抽取的2名學生中至少有一人得分在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設α是空間中的一個平面,l,m,n是三條不同的直線,則下列命題中正確的是( )
A.若mα,nα,l⊥m,l⊥n,則l⊥α
B.若mα,n⊥α,l⊥n,則l∥m
C.若l∥m,m⊥α,n⊥α,則l∥n
D.若l⊥m,l⊥n,則n∥m
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com