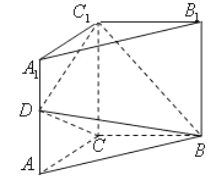
【題目】如圖，矩形ABCD中，
，
，F分別在線段BC和AD上，
，將矩形ABEF沿EF折起
記折起后的矩形為MNEF，且平面
平面ECDF．
Ⅰ
求證：
平面MFD；
Ⅱ若
，求證：
；
Ⅲ求四面體NFEC體積的最大值．
【答案】（1）見(jiàn)解析（2）見(jiàn)解析（3）
【解析】
試題分析：（1）證明：因?yàn)樗倪呅?/span>MNEF，EFDC都是矩形，所以MN∥EF∥CD，MN=EF=CD．
所以四邊形MNCD是平行四邊形，所以NC∥MD，因?yàn)?/span>NC平面MFD，所以NC∥平面MFD． 4分
（2）證明：連接ED，設(shè)ED∩FC=O．因?yàn)槠矫?/span>MNEF⊥平面ECDF，且NE⊥EF，所以NE⊥平面ECDF， 5分
所以FC⊥NE．又EC=CD，所以四邊形ECDF為正方形，所以 FC⊥ED．所以FC⊥平面NED，
所以ND⊥FC． 8分
（3）解：設(shè)NE=
，則EC=4-，其中0＜x＜4．由（1）得NE⊥平面FEC，所以四面體NFEC的體積為
，所以
.
當(dāng)且僅當(dāng)
，即x=2時(shí)，四面體NFEC的體積有最大值2．
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】某某大學(xué)藝術(shù)專業(yè)400名學(xué)生參加某次測(cè)評(píng)，根據(jù)男女學(xué)生人數(shù)比例，使用分層抽樣的方法從中隨機(jī)抽取了100名學(xué)生，記錄他們的分?jǐn)?shù)，將數(shù)據(jù)分成7組： 
，并整理得到如下頻率分布直方圖：
（Ⅰ）從總體的400名學(xué)生中隨機(jī)抽取一人，估計(jì)其分?jǐn)?shù)小于70的概率；
（Ⅱ）已知樣本中分?jǐn)?shù)小于40的學(xué)生有5人，試估計(jì)總體中分?jǐn)?shù)在區(qū)間[40,50）內(nèi)的人數(shù)；
（Ⅲ）已知樣本中有一半男生的分?jǐn)?shù)不小于70，且樣本中分?jǐn)?shù)不小于70的男女生人數(shù)相等．試估計(jì)總體中男生和女生人數(shù)的比例．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知
，且
，設(shè)命題
：函數(shù)
在
上單調(diào)遞減；命題
：函數(shù)
在
上為增函數(shù)，
（1）若“
且
”為真，求實(shí)數(shù)
的取值范圍
（2）若“
且
”為假，“
或
”為真，求實(shí)數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，直三棱柱 
中， 
, 
, 
是棱
上的動(dòng)點(diǎn).
證明： 
；
若平面
分該棱柱為體積相等的兩個(gè)部分，試確定點(diǎn)
的位置，并求二面角
的大小.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】下列命題中所有正確命題的序號(hào)為______．
若方程
表示圓，那么實(shí)數(shù)
；
已知函數(shù)
的圖象與函數(shù)
的圖象關(guān)于直線
對(duì)稱，令
，則
的圖象關(guān)于原點(diǎn)對(duì)稱；
在正方體
中，E、F分別是AB和
的中點(diǎn)，則直線CE、
F、DA三線共點(diǎn)；
冪函數(shù)的圖象不可能經(jīng)過(guò)第四象限．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】國(guó)家射擊隊(duì)的某隊(duì)員射擊一次，命中7~10環(huán)的概率如表所示：
命中環(huán)數(shù) | 10環(huán) | 9環(huán) | 8環(huán) | 7環(huán) |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求該射擊隊(duì)員射擊一次 求:
（1）射中9環(huán)或10環(huán)的概率；
（2）至少命中8環(huán)的概率；（3）命中不足8環(huán)的概率。
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知與曲線
相切的直線
，與
軸， 
軸交于
兩點(diǎn)， 
為原點(diǎn)， 
， 
，（ 
）.
（1）求證:： 
與
相切的條件是： 
.
（2）求線段
中點(diǎn)的軌跡方程；
（3）求三角形
面積的最小值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】設(shè)點(diǎn)
，動(dòng)圓
經(jīng)過(guò)點(diǎn)
且和直線
相切，記動(dòng)圓的圓心
的軌跡為曲線
.
（1）求曲線
的方程；
（2）設(shè)曲線
上一點(diǎn)
的橫坐標(biāo)為
，過(guò)
的直線交
于一點(diǎn)
，交
軸于點(diǎn)
，過(guò)點(diǎn)
作
的垂線交
于另一點(diǎn)
，若
是
的切線，求
的最小值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知函數(shù) 
．
（1）求函數(shù)y=f（x）的解析式，并用“五點(diǎn)法作圖”在給出的直角坐標(biāo)系中畫(huà)出函數(shù)y=f（x）在區(qū)間[0，π]上的圖象； 
（2）設(shè)α∈（0，π），f（ 
）= 
，求sinα的值．
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com