
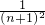 (n∈N*),設f(n)=(1-a1)(1-a2)(1-a3)…(1-an).
(n∈N*),設f(n)=(1-a1)(1-a2)(1-a3)…(1-an). ≥1.
≥1. ,f(2)=
,f(2)= ,f(3)=
,f(3)= ,f(4)=
,f(4)= .
.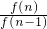 =1-an=1-
=1-an=1-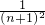 =
=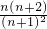 (n>1).
(n>1).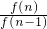
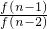 …
…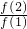 =
=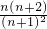
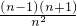
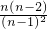 …
…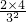 ,
,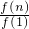 =
=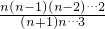 •
•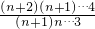 =
=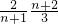 ,
,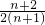 (n>1),又f(1)=
(n>1),又f(1)= 適合此式,
適合此式,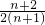 .
. ,
, +
+ +…+
+…+ ,
, +
+ +…+
+…+ .
. ,
, +
+ +…+
+…+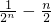 .
. +
+ +…+
+…+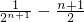 -(1+
-(1+ +
+ +…+
+…+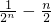 )
)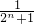 +
+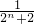 +…+
+…+ -
- .
.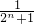 +
+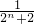 +…+
+…+ 的項數為2n,
的項數為2n,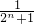 +
+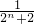 +…+
+…+ >
> +
+ +…+
+…+ =
=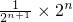 =
= ,
, =1
=1 ≥1.
≥1.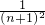 (n∈N*),分別令n=1,2,3,4.即可求得f(1)、f(2)、f(3)、f(4)的值;
(n∈N*),分別令n=1,2,3,4.即可求得f(1)、f(2)、f(3)、f(4)的值; +
+ +…+
+…+ .再設∅(n)=f(2n)-
.再設∅(n)=f(2n)- ,研究它的單調性,即數列{∅(n)}是單調遞增數列,從而求得其最小值為∅(1),從而得到∅(n)≥1即得g(2n)-
,研究它的單調性,即數列{∅(n)}是單調遞增數列,從而求得其最小值為∅(1),從而得到∅(n)≥1即得g(2n)- ≥1.
≥1.

科目:高中數學 來源: 題型:
| 1 | Sn |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 ,Tn為數列{bn}的前n項和,求Tn.
,Tn為數列{bn}的前n項和,求Tn.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com