
【題目】已知q和n均為給定的大于1的自然數,設集合M={0,1,2,…,q﹣1},集合A={x|x=x1+x2q+…+xnqn﹣1 , xi∈M,i=1,2,…n}.
(1)當q=2,n=3時,用列舉法表示集合A;
(2)設s,t∈A,s=a1+a2q+…+anqn﹣1 , t=b1+b2q+…+bnqn﹣1 , 其中ai , bi∈M,i=1,2,…,n.證明:若an<bn , 則s<t.
【答案】
(1)解:當q=2,n=3時,
M={0,1},A={x| ![]() ,xi∈M,i=1,2,3}.
,xi∈M,i=1,2,3}.
可得A={0,1,2,3,4,5,6,7}.
(2)證明:由設s,t∈A,s=a1+a2q+…+anqn﹣1,t=b1+b2q+…+bnqn﹣1,其中ai,bi∈M,i=1,2,…,n.an<bn,∴an﹣bn≤﹣1.
可得s﹣t=(a1﹣b1)+(a2﹣b2)q+…+ ![]() +
+ ![]()
≤﹣[1+q+…+qn﹣2+qn﹣1]
= ![]() <0.
<0.
∴s<t.
【解析】(1)當q=2,n=3時,M={0,1},A={x| ![]() ,xi∈M,i=1,2,3}.即可得到集合A.(2)由于ai , bi∈M,i=1,2,…,n.an<bn , 可得an﹣bn≤﹣1.由題意可得s﹣t=(a1﹣b1)+(a2﹣b2)q+…+
,xi∈M,i=1,2,3}.即可得到集合A.(2)由于ai , bi∈M,i=1,2,…,n.an<bn , 可得an﹣bn≤﹣1.由題意可得s﹣t=(a1﹣b1)+(a2﹣b2)q+…+ ![]() +
+ ![]() ≤﹣[1+q+…+qn﹣2+qn﹣1],再利用等比數列的前n項和公式即可得出.
≤﹣[1+q+…+qn﹣2+qn﹣1],再利用等比數列的前n項和公式即可得出.
【考點精析】關于本題考查的數列的前n項和,需要了解數列{an}的前n項和sn與通項an的關系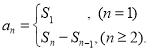 才能得出正確答案.
才能得出正確答案.


 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,點A1在平面ABC內的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2. 
(1)證明:AC1⊥A1B;
(2)設直線AA1與平面BCC1B1的距離為 ![]() ,求二面角A1﹣AB﹣C的大小.
,求二面角A1﹣AB﹣C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某人在垂直于水平地面ABC的墻面前的點A處進行射擊訓練.已知點A到墻面的距離為AB,某目標點P沿墻面上的射線CM移動,此人為了準確瞄準目標點P,需計算由點A觀察點P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,則tanθ的最大值是 . (仰角θ為直線AP與平面ABC所成角) 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列推理是類比推理的是( )
A. 由周期函數的定義判斷某函數是否為周期函數
B. 由![]() ,猜想任何一個小6的偶數都是兩個奇質數之和
,猜想任何一個小6的偶數都是兩個奇質數之和
C. 平面內不共線的3個點確定一個圓,由此猜想空間不共面的4個點確定一個球
D. 已知![]() 為定點,若動點P滿足
為定點,若動點P滿足![]() (其中
(其中![]() 為常數),則點
為常數),則點![]() 的軌跡為橢圓
的軌跡為橢圓
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學志愿者協會有6名男同學,4名女同學,在這10名同學中,3名同學來自數學學院,其余7名同學來自物理、化學等其他互不相同的七個學院,現從這10名同學中隨機選取3名同學,到希望小學進行支教活動(每位同學被選到的可能性相同).
(1)求選出的3名同學是來自互不相同學院的概率;
(2)設X為選出的3名同學中女同學的人數,求隨機變量X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】改革開放四十周年紀念幣從2018年12月5日起可以開始預約![]() 通過市場調查,得到該紀念章每1枚的市場價
通過市場調查,得到該紀念章每1枚的市場價![]() 單位:元
單位:元![]() 與上市時間
與上市時間![]() 單位:天
單位:天![]() 的數據如下:
的數據如下:
上市時間x天 | 8 | 10 | 32 |
市場價y元 | 82 | 60 | 82 |
![]() 根據上表數據,從下列函數:
根據上表數據,從下列函數:![]() ;
;![]() ;
;![]() 中選取一個恰當的函數刻畫改革開放四十周年紀念章的市場價y與上市時間x的變化關系并說明理由
中選取一個恰當的函數刻畫改革開放四十周年紀念章的市場價y與上市時間x的變化關系并說明理由
![]() 利用你選取的函數,求改革開放四十周年紀念章市場價最低時的上市天數及最低的價格.
利用你選取的函數,求改革開放四十周年紀念章市場價最低時的上市天數及最低的價格.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】蘇格蘭數學家納皮爾發明了對數表,這一發明為當時的天文學家處理“大數運算”做出了巨大貢獻![]() 法國著名數學家和天文學家拉普拉斯曾說過:“對數倍增了天文學家的壽命
法國著名數學家和天文學家拉普拉斯曾說過:“對數倍增了天文學家的壽命![]() ”比如在下面的部分對數表中,16,256對應的冪指數分別為4,8,冪指數和為12,而12對應的冪4096,因此
”比如在下面的部分對數表中,16,256對應的冪指數分別為4,8,冪指數和為12,而12對應的冪4096,因此![]() 根據此表,推算
根據此表,推算![]() ( )
( )
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
x | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2048 | 4096 | 8192 | 16384 | 32768 | 65536 | 131072 | 262144 | 524288 | 1048576 |
x | 21 | 22 | 23 | 24 | 25 | |||||
| 2097152 | 4194304 | 8388608 | 16777216 | 33554432 | |||||
A. 524288 B. 8388608 C. 16777216 D. 33554432
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩袋中各裝有大小相同的小球9個,其中甲袋中紅色、黑色、白色小球的個數分別為2個、3個、4個,乙袋中紅色、黑色、白色小球的個數均為3個,某人用左右手分別從甲、乙兩袋中取球.
(1)若左右手各取一球,問兩只手中所取的球顏色不同的概率是多少?
(2)若左右手依次各取兩球,稱同一手中兩球顏色相同的取法為成功取法,記兩次取球的成功取法次數為X,求X的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com