
【題目】已知函數![]() ,
, ![]() .
.
(1)求函數![]() 在點
在點![]() 點處的切線方程;
點處的切線方程;
(2)當![]() 時,求函數
時,求函數![]() 的極值點和極值;
的極值點和極值;
(3)當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 的極大值
的極大值![]() ,函數無極小值;(3)
,函數無極小值;(3)![]() .
.
【解析】試題分析:1)求出導函數,求解切線的斜率f′(1)=1﹣a,然后求解切線方程;
(2)求出函數的極值點,判斷函數的單調性,求解函數的極值即可;
(3)令g(x)=xlnx﹣a(x2﹣1)(x≥1),求出導函數g′(x)=lnx+1﹣2ax,令F(x)=g′(x)=lnx+1﹣2ax,求出![]() ,通過若a≤0,若
,通過若a≤0,若![]() ,若
,若![]() ,分別判斷函數的符號函數的單調性,求解函數的最值,然后求解a的取值范圍.
,分別判斷函數的符號函數的單調性,求解函數的最值,然后求解a的取值范圍.
試題解析:
(1)由題![]() ,所以
,所以![]() ,
,
所以切線方程為: ![]()
(2)由題![]() 時,
時, ![]() ,所以
,所以![]()
所以![]() ;
; ![]() ,
,
所以![]() 在
在![]() 單增,在
單增,在![]() 單減,所以
單減,所以![]() 在
在![]() 取得極大值
取得極大值![]() .
.
所以函數![]() 的極大值
的極大值![]() ,函數無極小值
,函數無極小值
(3)![]() ,令
,令![]() ,
,
![]() ,令
,令![]() ,
, ![]()
(1)若![]() ,
, ![]() ,
, ![]() 在
在![]() 遞增,
遞增, ![]()
∴![]() 在
在![]() 遞增,
遞增, ![]() ,從而
,從而![]() ,不符合題意
,不符合題意
(2)若![]() ,當
,當![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 遞增,
遞增,
從而![]() ,以下論證同(1)一樣,所以不符合題意
,以下論證同(1)一樣,所以不符合題意
(3)若![]() ,
, ![]() 在
在![]() 恒成立,
恒成立,
∴![]() 在
在![]() 遞減,
遞減, ![]() ,
,
從而![]() 在
在![]() 遞減,∴
遞減,∴![]() ,
, ![]() ,
,
綜上所述, ![]() 的取值范圍是
的取值范圍是![]() .
.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°. 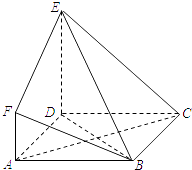
(1)求證:AC⊥平面BDE;
(2)設點M是線段BD上一個動點,試確定點M的位置,使得AM∥平面BEF,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年4月23日“世界讀書日”來臨之際,某校為了了解中學生課外閱讀情況,隨機抽取了100名學生,并獲得了他們一周課外閱讀時間(單位:小時)的數據,整理得到數據分組及頻數分布表.
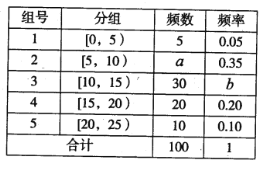
(Ⅰ)求![]() 的值,并作出這些數據的頻率分布直方圖;
的值,并作出這些數據的頻率分布直方圖;

(Ⅱ)假設每組數據組間是平均分布的,試估計該組數據的平均數;(同一組中的數據用該組區間的中點值作代表);
(Ⅲ)現從第3、4、5組中用分層抽樣的方法抽取6人參加校“中華詩詞比賽”,經過比賽后從這6人中選拔2人組成該校代表隊,求這2人來自不同組別的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年4月23日“世界讀書日”來臨之際,某校為了了解中學生課外閱讀情況,隨機抽取了100名學生,并獲得了他們一周課外閱讀時間(單位:小時)的數據,整理得到數據分組及頻數分布表.

(1)求![]() 的值,并作出這些數據的頻率分布直方圖;
的值,并作出這些數據的頻率分布直方圖;

(2)現從第3、4、5組中用分層抽樣的方法抽取6人參加校“中華詩詞比賽”,經過比賽后從這6人中選拔2人組成該校代表隊,求這2人來自不同組別的概率;
(3)假設每組數據組間是平均分布的,若該校希望使15%的學生的一周課外閱讀時間不低于![]() (小時)的時間,作為評選該校“課外閱讀能手”的依據,試估計該值
(小時)的時間,作為評選該校“課外閱讀能手”的依據,試估計該值![]() ,并說明理由.
,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司計劃投資A、B兩種金融產品,根據市場調查與預測,A產品的利潤與投資量成正比例,其關系如圖1,B產品的利潤與投資量的算術平方根成正比例,其關系如圖2(注:利潤與投資量的單位:萬元).
(1)分別將A、B兩產品的利潤表示為投資量的函數關系式;
(2)該公司已有10萬元資金,并全部投入A、B兩種產品中,問:怎樣分配這10萬元投資,才能使公司獲得最大利潤?其最大利潤為多少萬元?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2 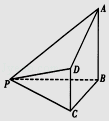
(1)證明:平面ABP⊥平面ADP;
(2)若直線PA與平面PCD所成角為α,求sinα的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近幾年,京津冀等地數城市指數“爆表”,尤其2015年污染最重.為了探究車流量與![]() 的濃度是否相關,現采集到北方某城市2015年12月份某星期星期一到星期日某一時間段車流量與
的濃度是否相關,現采集到北方某城市2015年12月份某星期星期一到星期日某一時間段車流量與![]() 的數據如表:
的數據如表:
時間 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
車流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散點圖知![]() 與
與![]() 具有線性相關關系,求
具有線性相關關系,求![]() 關于
關于的線性回歸方程;
(2)(ⅰ)利用(1)所求的回歸方程,預測該市車流量為8萬輛時![]() 的濃度;
的濃度;
(ⅱ)規定:當一天內![]() 的濃度平均值在
的濃度平均值在![]() 內,空氣質量等級為優;當一天內
內,空氣質量等級為優;當一天內![]() 的濃度平均值在
的濃度平均值在![]() 內,空氣質量等級為良.為使該市某日空氣質量為優或者為良,則應控制當天車流量在多少萬輛以內?(結果以萬輛為單位,保留整數.)
內,空氣質量等級為良.為使該市某日空氣質量為優或者為良,則應控制當天車流量在多少萬輛以內?(結果以萬輛為單位,保留整數.)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com