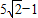一束光線從光源A(2,0)射到直線y=x+1上,經過反射,最后反射光線射到圓C1:x2+y2+8y+15=0上,求光線傳播到圓的最短路徑長為 .
【答案】
分析:設A關于y=x+1的對稱點為B,由對稱性可知AN=BN,所求光線傳播到圓的路徑長AN+NE=BN+NE,要使得其最小,則BE過圓心M(0,-4)時滿足條件,根據兩點間的距離公式可求
解答:解:如圖所示,設A關于y=x+1的對稱點為B,則可得B(-1,3),由對稱性可知AN=BN
所求光線傳播到圓的路徑長AN+NE=BN+NE,要使得其最小,則BE過圓心M(0,-4)時滿足條件
而BE=BM-ME=
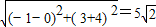
-1
故答案為:
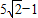
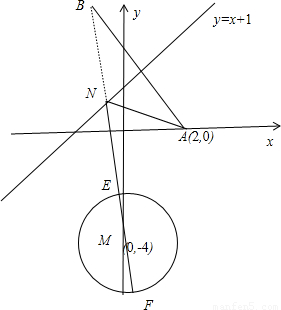 點評:
點評:本題主要考查了利用點與點關于直線對稱問題求解距離的最小值,解題的關鍵是要能夠發現A關于已知直線的對稱點B之后可知AN=BN,從而問題轉化為求解在圓外一點B,使得點B到圓上一點的距離最小(大)

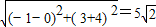 -1
-1