
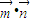 },其中
},其中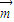 =(2x-b,1),
=(2x-b,1),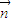 =(1,b+1),點列Pn(an,bn)(n∈N+)在L中,p1為L與y軸的交點,數列{an}是公差為1的等差數列.
=(1,b+1),點列Pn(an,bn)(n∈N+)在L中,p1為L與y軸的交點,數列{an}是公差為1的等差數列. ,令Sn=f(1)+f(2)+f(3)+…+f(n),試寫出Sn關于n的表達式;
,令Sn=f(1)+f(2)+f(3)+…+f(n),試寫出Sn關于n的表達式; ,給定奇數m(m為常數,m∈N+,m>2).是否存在k∈N+,,使得
,給定奇數m(m為常數,m∈N+,m>2).是否存在k∈N+,,使得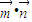 =(2x-b)+(b+1)=2x+1,然后再根據等差通項公式得an=a1+(n-1)×1=n-1,最后在根據bn=2an+1,得bn=2n-1
=(2x-b)+(b+1)=2x+1,然后再根據等差通項公式得an=a1+(n-1)×1=n-1,最后在根據bn=2an+1,得bn=2n-1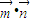 =(2x-b)+(b+1)=2x+1
=(2x-b)+(b+1)=2x+1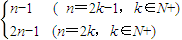
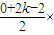 k+
k+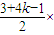 k=3k2.
k=3k2.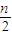 .所以
.所以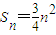
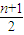 .所以Sn=
.所以Sn=
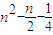 .
.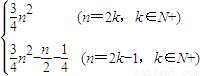 .
. 與k∈N+矛盾;(11分)
與k∈N+矛盾;(11分)

 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:
| m |
| n |
| m |
| n |
| ||
n|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| m |
| n |
| m |
| n |
|
| Sn |
| S2n |
查看答案和解析>>
科目:高中數學 來源: 題型:
| m |
| n |
| m |
| n |
| ||
| n•|P1Pn| |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中數學 來源: 題型:
| m |
| n |
| m |
| n |
|
| 1 |
| |P1P2|2 |
| 1 |
| |P1P3|2 |
| 1 |
| |P1Pn|2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| m |
| n |
| m |
| n |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com