
(12分)(2011•湖北)提高過江大橋的車輛通行能力可改善整個城市的交通狀況,在一般情況下,大橋上的車流速度v(單位:千米/小時)是車流密度x(單位:輛/千米)的函數,當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時,研究表明:當20≤x≤200時,車流速度v是車流密度x的一次函數.
(Ⅰ)當0≤x≤200時,求函數v(x)的表達式;
(Ⅱ)當車流密度x為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)f(x)=x•v(x)可以達到最大,并求出最大值.(精確到1輛/小時).
(I) 函數v(x)的表達式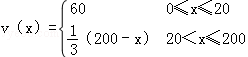
(II) 當車流密度為100輛/千米時,車流量可以達到最大值,最大值約為3333輛/小時.
解析試題分析:(I)根據題意,函數v(x)表達式為分段函數的形式,關鍵在于求函數v(x)在20≤x≤200時的表達式,根據一次函數表達式的形式,用待定系數法可求得;
(II)先在區間(0,20]上,函數f(x)為增函數,得最大值為f(20)=1200,然后在區間[20,200]上用基本不等式求出函數f(x)的最大值,用基本不等式取等號的條件求出相應的x值,兩個區間內較大的最大值即為函數在區間(0,200]上的最大值.
解:(I) 由題意:當0≤x≤20時,v(x)=60;當20<x≤200時,設v(x)=ax+b
再由已知得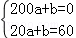 ,解得
,解得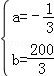
故函數v(x)的表達式為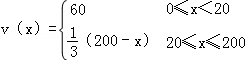
(II)依題并由(I)可得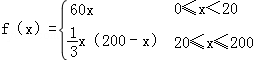
當0≤x<20時,f(x)為增函數,故當x=20時,其最大值為60×20=1200
當20≤x≤200時,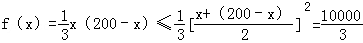
當且僅當x=200﹣x,即x=100時,等號成立.
所以,當x=100時,f(x)在區間(20,200]上取得最大值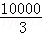 .
.
綜上所述,當x=100時,f(x)在區間[0,200]上取得最大值為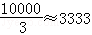 ,
,
即當車流密度為100輛/千米時,車流量可以達到最大值,最大值約為3333輛/小時.
答:(I) 函數v(x)的表達式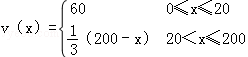
(II) 當車流密度為100輛/千米時,車流量可以達到最大值,最大值約為3333輛/小時.
點評:本題主要考查函數、最值等基礎知識,同時考查運用數學知識解決實際問題的能力,屬于中等題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
某房地產開發公司計劃在一樓區內建造一個長方形公園ABCD,公園由長方形休閑區A1B1C1D1和環公園人行道(陰影部分)組成.已知休閑區A1B1C1D1的面積為4000m2,人行道的寬分別為4m和10m(如圖所示).
(1)若設休閑區的長和寬的比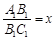 ,求公園ABCD所占面積S關于x的函數解析式;
,求公園ABCD所占面積S關于x的函數解析式;
(2)要使公園所占面積最小,休閑區A1B1C1D1的長和寬應如何設計?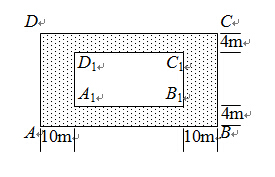
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有一種密英文的明文(真實文)按字母分解,其中英文的a,b,c, ,z的26個字母(不分大小寫),依次對應1,2,3, ,26這26個自然數,見如下表格:
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
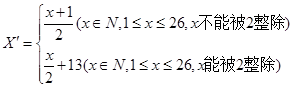
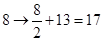 ,即
,即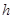 變成
變成 ;如
;如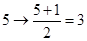 ,即
,即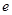 變成
變成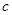 .
.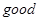 譯成的密文是什么?
譯成的密文是什么? ,那么原來的明文是什么?
,那么原來的明文是什么?查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于函數f(x)若存在x0∈R,f(x0)=x0成立,則稱x0為f(x)的不動點.已知f(x)=ax2+(b+1)x+b-1(a≠0).
(1)當a=1,b=-2時,求函數f(x)的不動點;
(2)若對任意實數b,函數f(x)恒有兩個相異的不動點,求a的取值范圍;
(3)在(2)的條件下,若y=f(x)圖象上A,B兩點的橫坐標是函數f(x)的不動點,且A,B兩點關于直線y=kx+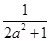 對稱,求b的最小值.
對稱,求b的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=3x-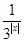 .
.
(1)若f(x)=2,求x的值;
(2)判斷x>0時,f(x)的單調性;
(3)若3tf(2t)+mf(t)≥0對于t∈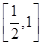 恒成立,求m的取值范圍.
恒成立,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某加油站擬造如圖所示的鐵皮儲油罐(不計厚度,長度單位:米),其中儲油罐的中間為圓柱形,左右兩端均為半球形,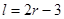 (
(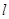 為圓柱的高,
為圓柱的高,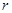 為球的半徑,
為球的半徑,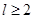 ).假設該儲油罐的建造費用僅與其表面積有關.已知圓柱形部分每平方米建造費用為
).假設該儲油罐的建造費用僅與其表面積有關.已知圓柱形部分每平方米建造費用為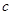 千元,半球形部分每平方米建造費用為3千元.設該儲油罐的建造費用為
千元,半球形部分每平方米建造費用為3千元.設該儲油罐的建造費用為 千元.
千元.
(1)寫出 關于
關于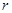 的函數表達式,并求該函數的定義域;
的函數表達式,并求該函數的定義域;
(2)求該儲油罐的建造費用最小時的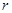 的值.
的值.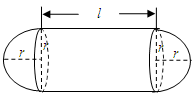
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)的圖象與函數h(x)=x+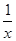 +2的圖象關于點A(0,1)對稱.
+2的圖象關于點A(0,1)對稱.
(1)求f(x)的解析式;
(2)若g(x)=f(x)·x+ax,且g(x)在區間[0,2]上為減函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于函數 ,若在定義域存在實數
,若在定義域存在實數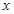 ,滿足
,滿足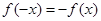 ,則稱
,則稱 為“局部奇函數”.
為“局部奇函數”.
(1)已知二次函數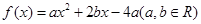 ,試判斷
,試判斷 是否為“局部奇函數”?并說明理由;
是否為“局部奇函數”?并說明理由;
(2)設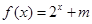 是定義在
是定義在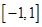 上的“局部奇函數”,求實數
上的“局部奇函數”,求實數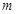 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com