
若![]() ,
,![]() ,
,![]() ,
,![]() 為常數,且
為常數,且
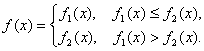
(Ⅰ)求![]() 對所有實數成立的充要條件(用
對所有實數成立的充要條件(用![]() 表示);
表示);
(Ⅱ)設![]() 為兩實數,
為兩實數,![]() 且
且![]()
![]()
![]() ,若
,若![]()
求證:![]() 在區間
在區間![]() 上的單調增區間的長度和為
上的單調增區間的長度和為![]() (閉區間
(閉區間![]() 的長度定義為
的長度定義為![]() ).
).
解:(Ⅰ)![]() 恒成立
恒成立
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]() (*)
(*)
因為![]() ,
,
所以,故只需![]()
![]() (*)恒成立.
(*)恒成立.
綜上所述,![]() 對所有實數成立的充要條件是
對所有實數成立的充要條件是![]()
![]() . ………4分
. ………4分
(Ⅱ)1°如果![]()
![]() ,則的圖象關于直線
,則的圖象關于直線![]() 對稱.因為
對稱.因為![]() ,所以區間
,所以區間![]() 關于直線
關于直線![]() 對稱.
對稱.
因為減區間為![]() ,增區間為
,增區間為![]() ,所以單調增區間的長度和為
,所以單調增區間的長度和為![]() . ………6分
. ………6分
2°如果![]()
![]() .
.
(1)當![]()
![]() 時.
時.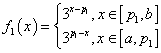 ,
,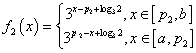
當![]() ,
,![]() 因為
因為![]() ,所以
,所以![]() ,故
,故![]() =
=![]() .
.
當![]() ,
,![]() 因為
因為![]() ,所以
,所以![]() ,故
,故![]() =
=![]() .
.
因為![]() ,所以
,所以![]() ,所以
,所以![]() 即
即
![]() .
.
當![]() 時,令
時,令![]() ,則
,則![]() ,所以
,所以![]() ,
,
當![]() 時,
時,![]() ,所以
,所以![]() =
=![]() ;
;
![]() 時,
時,![]() ,所以
,所以![]() =
=![]() .
.
![]() 在區間
在區間![]() 上的單調增區間的長度和
上的單調增區間的長度和![]()
=![]() . …………10分
. …………10分
(2)當![]()
![]() 時.
時.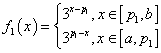 ,
,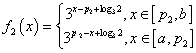
當![]() ,
,![]() 因為
因為![]() ,所以
,所以![]() ,故
,故![]() =
=![]() .
.
當![]() ,
,![]() 因為
因為![]() ,所以
,所以![]() ,故
,故![]() =
=![]() .
.
因為![]() ,所以
,所以![]() ,所以
,所以![]() .
.
當![]() 時,令
時,令![]() ,則
,則![]() ,所以
,所以![]() ,
,
當![]() 時,
時, ![]() ,所以
,所以![]() =
=![]() ;
;
![]() 時,
時,![]() ,所以
,所以![]() =
=![]() ;
;
![]() 在區間
在區間![]() 上的單調增區間的長度和
上的單調增區間的長度和![]()
=![]() .
.
綜上得![]() 在區間
在區間![]() 上的單調增區間的長度和為
上的單調增區間的長度和為![]() . …………14分
. …………14分


科目:高中數學 來源: 題型:
| x-m |
| f(x) |
| x |
查看答案和解析>>
科目:高中數學 來源:2012年北京市西城區高考數學一模試卷(文科)(解析版) 題型:解答題
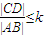 ,其中k為常數,且0<k<1,求S的最大值.
,其中k為常數,且0<k<1,求S的最大值.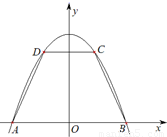
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com