已知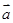
＝（2，1），
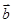＝（－3，4），則3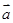＋4＝ ．
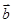科目：高中數學 來源：河南省衛輝市第一中學2012屆高三4月考試數學理科試題 題型：047
已知|x1－2|＜1，|x2－2|＜1．
(Ⅰ)求證：2＜x1＋x2＜6，|x1－x2|＝2；
(Ⅱ)若f(x)＝x2－x＋1，求證：|x1－x2|＜|f(x1)－f(x2)|＜5|x1－x2|．
查看答案和解析>>
科目：高中數學 來源： 題型：
(本小題滿分14分)
在△OAB的邊OA,OB上分別有一點P,Q,已知
:
＝1:2, 
:
＝3:2,連結AQ,BP,設它們交于點R,若
＝a，
＝b.
(1)用a與 b表示
；
(2)過R作RH⊥AB,垂足為H,若| a|＝1, | b|＝2, a與 b的夾角
的取值范圍.
查看答案和解析>>
科目：高中數學 來源：2014屆廣東省高一期中考試文科數學試卷A卷（解析版） 題型：解答題
已知函數f(x)(x∈R)滿足f(x)＝
，a≠0，f(1)＝1，且使f(x)＝2x成立的實數x只有一個．
(1)求函數f(x)的表達式；
(2)若數列{an}滿足a1＝
，an+1＝f(an)，bn＝
－1，n∈N*，證明數列{bn}是等比數列，并求出{bn}的通項公式；
(3)在(2)的條件下，證明：a1b1＋a2b2＋…＋anbn<1(n∈N*)．
【解析】解： (1)由f(x)＝，f(1)＝1，得a＝2b＋1.
由f(x)＝2x只有一解，即＝2x，
也就是2ax2－2(1＋b)x＝0(a≠0)只有一解，
∴b＝－1.∴a＝－1.故f(x)＝
.…………………………………………4分
(2)an＋1＝f(an)＝
(n∈N*)，bn＝－1， ∴
＝
＝
＝
，
∴{bn}為等比數列，q＝.又∵a1＝，∴b1＝
－1＝，
bn＝b1qn－1＝
n－1＝n(n∈N*)．……………………………9分
(3)證明：∵anbn＝an
＝1－an＝1－
＝
，
∴a1b1＋a2b2＋…＋anbn＝
＋
＋…＋<
＋
＋…＋
＝
＝1－<1(n∈N*)．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
＝（2，1），
＝（－3，4），∴3
＝（2,1）, 
＝10, 
＝
,則
＝
（ ）
B．
C．5 D．25