Question

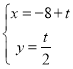【題目】在平面坐標系中中，已知直線l的參考方程為（t為參數(shù)），曲線C的參數(shù)方程為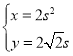（s為參數(shù)）.設P為曲線C上的動點，

（Ⅰ）求直線l和曲線C的直角坐標方程；

（Ⅱ）求點P到直線l的距離的最小值.

Answer 1

【答案】（Ⅰ），（Ⅱ）

【解析】

（Ⅰ）由直線的參數(shù)方程為為參數(shù)），消去參數(shù)，可得普通方程．由曲線的參數(shù)方程為為參數(shù)）．消去參數(shù)，可得曲線直角坐標方程．（Ⅱ）設點，則為參數(shù)）．利用點到直線的距離公式可得：，利用二次函數(shù)的單調(diào)性即可得出最小值．

（Ⅰ）由直線的參數(shù)方程為為參數(shù)），消去參數(shù)，可得：．

所以直線直角坐標方程為．

由曲線的參數(shù)方程為為參數(shù)）．消去參數(shù)，可得：．

所以曲線直角坐標方程為．

（Ⅱ）設點，則為參數(shù)）．

則．

當時取等號，此時，，

所以點到直線的距離的最小值為．