
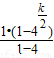 =
= (2k-1),
(2k-1), (2k-1).
(2k-1). (4n-1).
(4n-1). (4n-1).
(4n-1).

 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:北京市西城區2012屆高三4月第一次模擬考試數學文科試題 題型:044
對于數列A:a1,a2,a3(ai∈N,i=1,2,3),定義“T變換”:T將數列A變換成數列B:b1,b2,b3,其中bi=|ai-ai+1|(i=1,2),且b3=|a3-a1|.這種“T變換”記作B=T(A).繼續對數列B進行“T變換”,得到數列C:c1,c2,c3,依此類推,當得到的數列各項均為0時變換結束.
(Ⅰ)試問A:2,6,4經過不斷的“T變換”能否結束?若能,請依次寫出經過“T變換”得到的各數列;若不能,說明理由;
(Ⅱ)設A:a1,a2,a3,B=T(A).若B:b,2,a(a≥b),且B的各項之和為2012.
(ⅰ)求a,b;
(ⅱ)若數列B再經過k次“T變換”得到的數列各項之和最小,求k的最小值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2012年北京市西城區高考數學一模試卷(文科)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com