
(04年浙江卷文)(12分)
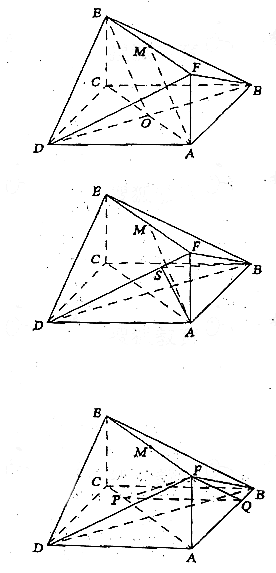
如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直, AB=![]() ,AF=1,M是線段EF的中點。
,AF=1,M是線段EF的中點。
(Ⅰ)求證AM∥平面BDE;
(Ⅱ)求證AM⊥平面BDF;
(Ⅲ)求二面角A―DF―B的大小;

解析: 方法一(Ⅰ)記AC與BD的交點為O,連接OE,
∵O、M分別是AC、EF的中點,ACEF是矩形,
∴四邊形AOEM是平行四邊形,
∴AM∥OE。
∵![]() 平面BDE,
平面BDE, ![]() 平面BDE,
平面BDE,
∴AM∥平面BDE。
(Ⅱ)在平面AFD中過A作AS⊥DF于S,連結BS,
∵AB⊥AF, AB⊥AD, ![]()
∴AB⊥平面ADF,
∴AS是BS在平面ADF上的射影,
由三垂線定理得BS⊥DF。
∴∠BSA是二面角A―DF―B的平面角。
在RtΔASB中,![]()
∴![]()
∴二面角A―DF―B的大小為60º。
(Ⅲ)設CP=t(0≤t≤2),作PQ⊥AB于Q,則PQ∥AD,
∵PQ⊥AB,PQ⊥AF,![]() ,
,
∴PQ⊥平面ABF,![]() 平面ABF,
平面ABF,
∴PQ⊥QF。
在RtΔPQF中,∠FPQ=60º,
PF=2PQ。
∵ΔPAQ為等腰直角三角形,
∴![]()
又∵ΔPAF為直角三角形,
∴![]() ,
,
∴![]()
所以t=1或t=3(舍去)
即點P是AC的中點。
方法二
(Ⅰ)建立如圖所示的空間直角坐標系。
設![]() ,連接NE,
,連接NE,
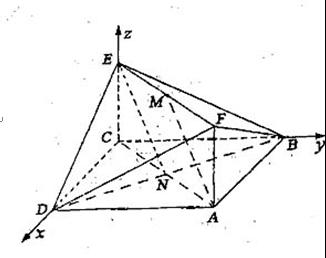
則點N、E的坐標分別是(![]() 、(0,0,1),
、(0,0,1),
∴NE=(![]() ,
,
又點A、M的坐標分別是
(![]() )、(
)、(![]()
∴ AM=(![]()
∴NE=AM且NE與AM不共線,
∴NE∥AM。
又∵![]() 平面BDE,
平面BDE, ![]() 平面BDE,
平面BDE,
∴AM∥平面BDF。
(Ⅱ)∵AF⊥AB,AB⊥AD,AF![]()
∴AB⊥平面ADF。
∴![]() 為平面DAF的法向量。
為平面DAF的法向量。
∵NE?DB=(![]() ?
?![]() =0,
=0,
∴NE?NF=(![]() ?
?![]() =0得
=0得
NE⊥DB,NE⊥NF,
∴NE為平面BDF的法向量。
∴cos<AB,NE>=![]()
∴AB與NE的夾角是60º。
即所求二面角A―DF―B的大小是60º。
(Ⅲ)

設P(t,t,0)(0≤t≤![]() )得
)得
![]()
∴CD=(![]() ,0,0)
,0,0)
又∵PF和CD所成的角是60º。
∴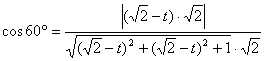
解得![]() 或
或![]() (舍去),
(舍去),
即點P是AC的中點。


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com